The (submicron + micron) bimodal size SiCp-reinforced Mg matrix composite was compressed at the temperature of 270-420 °C and strain rate of 0.001-1 s-1. Then, dynamic recrystallization (DRX) behavior of the composite was investigated by thermodynamic method and verified by microstructure analysis. Results illustrated that the composite possess the lower critical strain and higher DRX ratio as compared to monolithic Mg alloys during hot deformation process. The predicted DRX ratio increased with the proceeding of compression, which was well consistent with the experimental value. Results from thermodynamic calculation suggested that the occurrence of DRX could be promoted by SiCp, which would be further proved by microstructure analysis. Formation of particle deformation zone around micron SiCp played a significant role in promoting DRX nucleation. Nevertheless, the distribution of submicron SiCp was increasingly uniform with the proceeding of compression, which could fully restrain grain growth. Therefore, the corporate effects of micron and submicron SiCp on DRX contributed to the improvement of DRXed ratio and the refinement of grain size for the composite during compression process.
As the lightest material in nature, magnesium alloys possess great potential in the application of automotive, defenses and aerospace fields, etc. [1]. For the low stacking fault energy, dynamic recrystallization (DRX) plays an important role in magnesium alloys during hot deformation process based on the works of Al-samman et al. [2] and Zhou et al. [3]. Meanwhile, the microstructural variation affected by DRX during hot deformation can be reflected on the stress-strain curves directly. On the previous investigation of Wang et al. [4], occurrence of DRX was identified as the appearance of a peak in stress-strain curves [4]. Once the DRX was activated, an additional softening could be observed in the curve, and then, the stress went down until a steady state is reached.
On the researches of Sakai et al. [5] and Busso et al. [6], the presence of stress peak in the stress-strain curves was often considered as a reliable signal for the onset of DRX. However, the DRX was emerged before stress peak according to the investigation of fundamental dynamic softening mechanisms of Sah et al. [7]. Usually, the strain for DRX is known as critical strain, which depends on the composition of the material, grain size prior to deformation and deformation parameters (temperature and strain rate) [5]. Therefore, the critical strain obtained by stress-strain curves is particularly important for the investigation of DRX. Poliak et al. [8] proposed an irreversible thermodynamics principle to estimate critical condition for DRX. Fatemi-Varzaned et al. [9] gave the relationship among the DRX ratio, flow stress, peak stress and steady-state stress in AZ31 alloy. The evolution of DRX grains during hot deformation had been depicted based on the investigation of the dynamic recrystallization behavior for AZ31 alloy by Liu et al. [10]. However, few attention has been made in this aspect of particle-reinforced magnesium matrix composite (PMMCs) at present.
Up to now, a lot of works have been done on the hot deformation behavior of PMMCs. The dynamic recrystallization behavior during hot deformation of 0.2 μ mSiCp-reinforced Mg matrix composite had been studied by Deng et al. [11], which showed that the 0.2 μ mSiCp could not only pin dislocation, but also help to generate dislocations owing to the deformation mismatch between matrix and particles, thus causing the increase in dislocation density around SiCp, which benefit to stimulate DRX nucleation. The DRX of 10 μ mSiCp/AZ91 composite compressed at different strains, strain rates and temperatures was studied by Wang et al. [12], and it was found that the particle deformation zone (PDZ) formed near 10 μ mSiCp was considered as an ideal site for DRX. Besides, it was also noted that the DRX behavior of Mg matrix strongly depended on particle size [13]. According to the investigations of Laurent et al. [14] and Doherty et al. [15], the stimulating effect of PDZ on DRXed nucleation only occurred when the size of particles was larger than 1 μ m. As the particle size was smaller than 1 μ m, the PDZ formed around particle could be negligible, and thus, the DRX mechanism influenced by fine particles will be different from that of larger particles. Therefore, the bimodal size (< 1 + > 1 μ m) particles may have various impacts on DRX as compared to that of single-sized particles. In the previous work [16] about the microstructure and strengthening mechanism of bimodal size particle-reinforced magnesium matrix composite, the bimodal size SiCp reflected obvious impact on refining grain size, and yet, the DRX behavior of Mg matrix influenced by bimodal size SiCp is still unclear.
As a consequence, the thermodynamic analysis is utilized on the true strain-stress curves of [1.5 vol% (0.2 μ m) + 8.5 vol% (10 μ m)] bimodal size SiCp/AZ91 magnesium matrix composite. In accordance with observing and analyzing the microstructure evolution of monolithic AZ91 alloy and bimodal size SiCp-reinforced magnesium matrix composite during hot compression process, the DRX behavior of Mg matrix influenced by bimodal size SiCp will be established.
The material used in the present study is AZ91 alloy reinforced by two sizes of SiCp. One size of the particle is ~0.2 μ m with the fraction of 1.5 vol%, and the other is ~10 μ m with the fraction of 8.5 vol%. Thus, the total fraction of SiCp used in the present work is 10 vol%. For simplification, the [1.5 vol% (0.2 μ m) + 8.5 vol% (10 μ m)] bimodal size SiCp/AZ91 magnesium matrix composite is denoted as “ S-1.5 + 10-8.5, ” and the composite was fabricated by stir casting, the details of which had been reported in Ref. [16].
The compressive tests were conducted by Gleeble-3500D test machine. The compression temperature was 270-420 ° C, and strain rate was 0.001-1 s-1. All specimens were consecutively heated to the designed temperature at a heating rate of 5 ° C/s and kept at the temperature for 5 min to ensure that the specimens were homogeneous in temperature. After the specimens were deformed to the true strain of ε = 0.5, they were quenched in water as quickly as possible.
Microstructure observation was carried out by 4XC optical microscope (OM) and MIRA 3XMU scanning electron microscope (SEM). The specimens for OM were cut parallel to compression direction. Then, they would be ground, polished and etched in acetic picral [5 mL acetic acid + 6 g picric acid + 10 mL H2O + 100 mL ethanol (95 vol%)]. The average DRXed grain size and the volume fraction of DRXed grains (XDRX) were measured by the Image Pro-Plus software. The XDRX is defined as XDRX = ∑ Af/∑ Ai, where Af denotes the area of DRXed grains, and Ai denotes the area of metallographs.
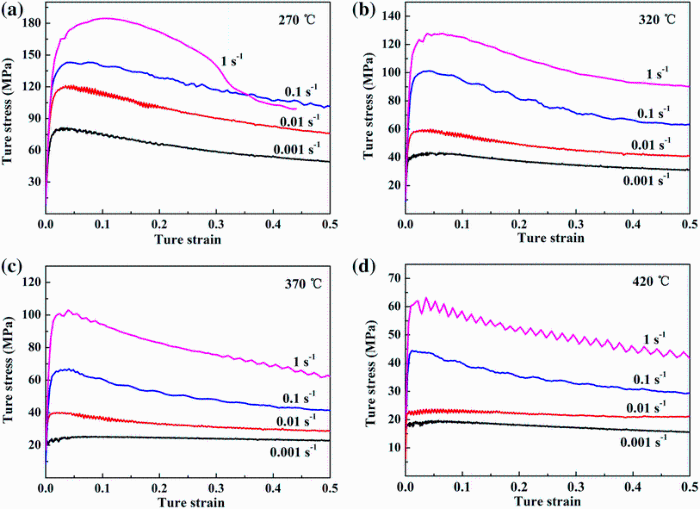
The true stress-true strain curves of S-1.5 + 10-8.5 composite at different temperatures and strain rates are shown in Fig. 1. All the curves exhibit an identical characteristic that the stress rises and then declines after a peak value during hot compression process. Rapid increase in the stress at the initial stage of compression indicates the occurrence of work hardening caused by the generation and multiplication of dislocations [17]. Once the DRX is activated, obvious work softening is occurred [18]. Besides, the true stress-strain curves are affected significantly by the temperature. Figure 1 demonstrates that the flow stress declines with the temperature rising at any given strain rate. For a given temperature, the flow stress increases with the increase in strain.
Usually, the generation and pileup of dislocations lead to work hardening at the primary stage of compression process, and then, it achieved a balance coupled with work softening, which are caused by DRX [4]. The variation of microstructure affected by DRX during hot compression may directly reflect on the changes of true stress (σ )-true strain (ε ) curves. Thus, the strain corresponding to critical stress can be used to infer the original point of DRX. As a matter of fact, the work hardening rate (θ ) during compression process can be described by θ = dσ /dε . The onset point for DRX may be detected from the inflections of θ -σ curve, which directly reflect on the convex shape of true stress-true strain curve [19]. Figure 2 shows the θ -σ curves of S-1.5 + 10-8.5 composite at various compression conditions. All the curves in Fig. 2 demonstrate a downward inflection, which correspond to the peak (θ = 0) and post-peak softening (θ < 0), respectively. And this is thought to be caused by the occurrence of DRX.
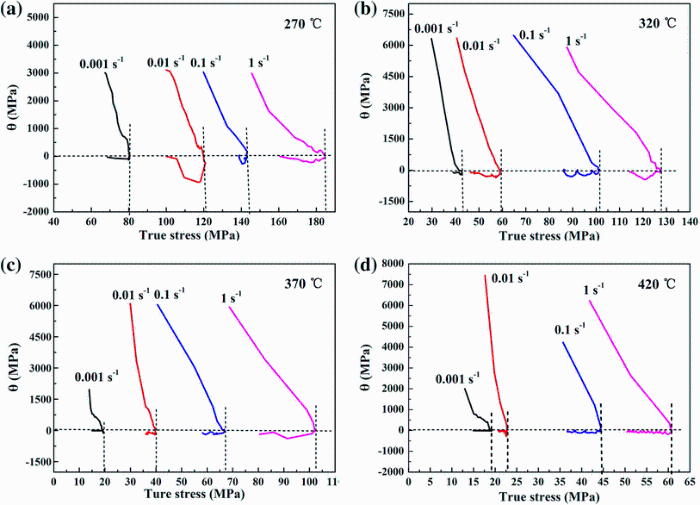 | Fig. 2 The θ -σ plots of the S-1.5 + 10-8.5 composite based on Fig. 1 |
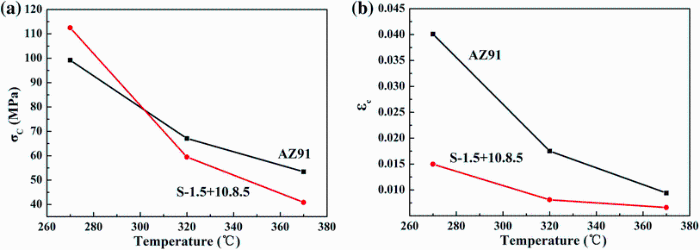
On Poliak et al’ s investigation [8], an estimated critical condition for DRX based on the irreversible thermodynamics principle had been proposed. By differentiating the dθ /dσ and σ , a distinct minimum value can be obtained in the dθ /dσ -σ curve. The true stress corresponding to the minimum value is taken as critical stress. Figure 3 shows the dθ /dσ -σ curves of S-1.5 + 10-8.5 composite in various compression conditions. The obtained critical stress (σ c) from Fig. 3 is summarized in Fig. 4a. It suggests that the σ c value rises with the increase in strain rate and the decrease in compression temperature. According to σ c value, the critical strain (ε c) can also be deduced from the true stress-strain curves in Fig. 1. Figure 4b illustrates the correlation between ε c and strain rate. The variation tendency of ε c is similar to σ c, and both of them rise with the increase in strain rate and the decrease in temperature.
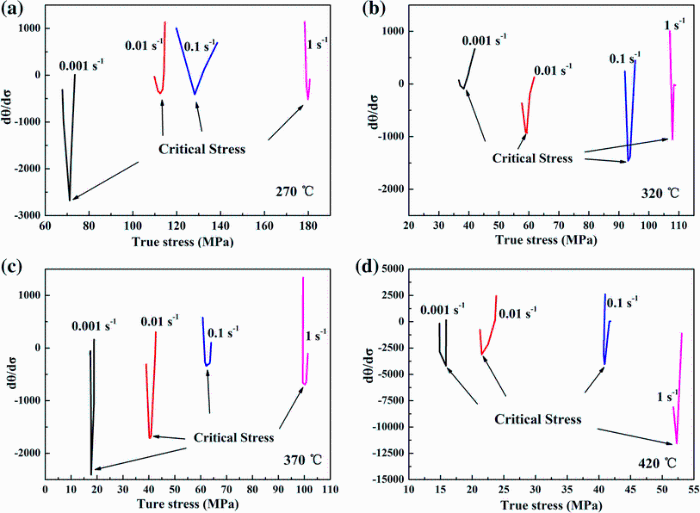 | Fig. 3 Relationship between dθ /dσ and σ of S-1.5 + 10-8.5 composite based on Fig. 2 |
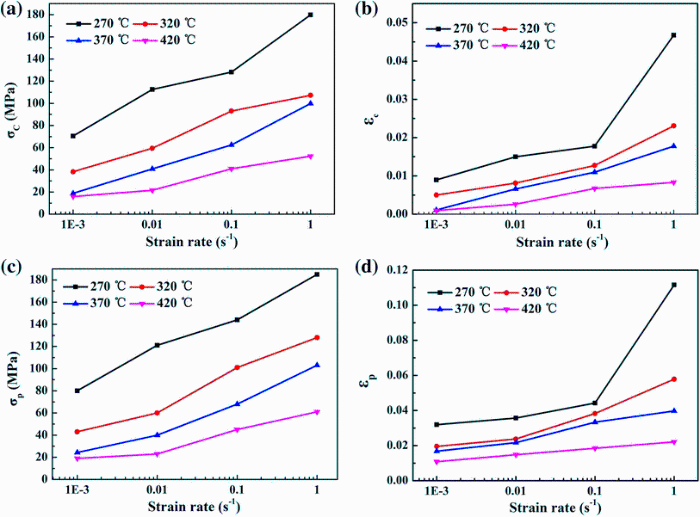 | Fig. 4 Relationship of strain rate ἐ versus critical stress σ ca, critical strain ε cb, peak stress σ pc, peak strain ε pd |
To further study σ c and ε c, the values of σ p (peak stress) and ε p (peak strain) extracted from Fig. 1 are demonstrated in Fig. 4c and d, respectively. In comparison with Fig. 4a-d, the σ c value is lower than σ p, while the ε c value is lower than ε p, respectively. Above phenomenon proves that the DRX occurs before the peak stress and peak strain appear. With the increase in temperature and decrease in strain rate, the atomic activity improves and the movement of the non-basal plane slip systems becomes much easier, which may result in the decrease in both σ c and σ p values, as shown in Fig. 4.
To reveal the effect of SiCp on the critical stress and strain for DRX, AZ91 alloy as a comparison was compressed at the temperature of 270-370 ° C and the strain rate of 0.01 s-1, and the results are summarized in Fig. 5. It shows that σ c and ε c decrease with the increase in temperature in AZ91 alloy and S-1.5 + 10-8.5 composite. At 270 ° C, the σ c of S-1.5 + 10-8.5 composite is slightly higher than that of AZ91 alloy; however, it becomes lower when the temperature increased to 320 and 370 ° C, as shown in Fig. 5a. Figure 5b shows that the ε c of S-1.5 + 10-8.5 composite is lower than that of AZ91 alloy at any temperature. Above comparison reveals that the addition of SiCp plays pronounced effect on reducing σ c and ε c for DRX.
Hot compression process is proceeding with the continual generation and multiplication of dislocations, as well as the nucleation and growth of DRXed grains [20]. Once the accumulated strain exceeds ε c value, the DRX is occurred. According to the Avrami function, the volume fraction of DRXed grains during hot compression process can be depicted by [10]:
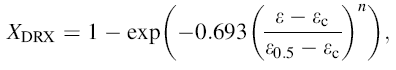 |
where the XDRX is the DRXed ratio, ε is the true strain, ε c is the critical strain for DRX, and n is the material constant. ε 0.5 is the strain for 50% DRX which can be calculated by [10]:
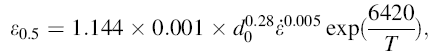 |
whered0 is the average size of DRXed grains. As mentioned above, the generation and pileup of dislocations lead to work hardening at the primary stage of compression process, and then, it achieves a balance coupled with work softening caused by DRX. Once the work hardening is balanced with work softening during compression process, the steady-state appears. Based on the flow stress σ , peak stress σ p and steady-state stress σ s, the XDRX can also be described by [9]:
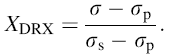 |
By Eqs. (1) and (3), n in different conditions is obtained by regression analysis, as demonstrated in Table 1. According to Eqs. (1-3), the XDRX affected by strain, temperature and strain rate is summarized in Fig. 6. As the strain rate is 1 s-1 and strain is 0.1, the calculated XDRX is ~38% at 270 ° C, and it increases to ~94% as the temperature is 420 ° C. When the strain rate decreased from 1 s-1 to 0.001 s-1, the XDRX enhanced from ~38% to ~54%, at the temperature of 270 ° C and strain of 0.1. As the strain increased from 0.1 to 0.5, the XDRX enhances significantly, as shown in Fig. 6. At the strain rate of 1 s-1, the compression process only lasts 10 s when the strain increased to 0.5; however, the XDRX can reach ~90% and ~98% at 270 ° C and 420 ° C, respectively, which indicates the nearly completed DRX in the S-1.5 + 10-8.5 composite after hot compression.
| Table 1 Calculated n values at different temperatures and strain rates |
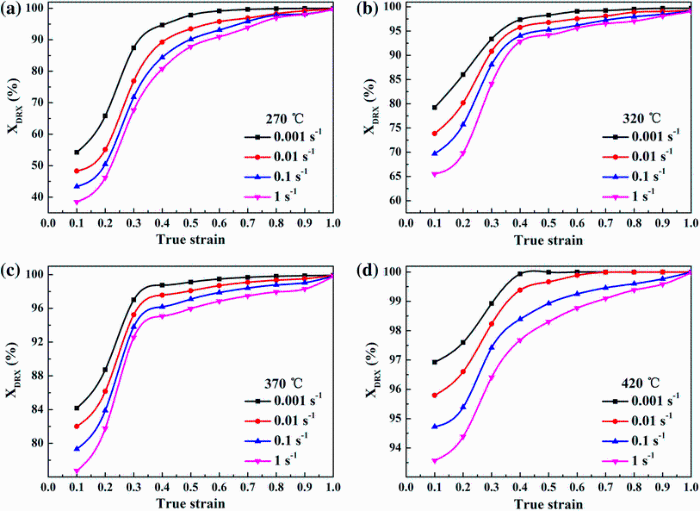 | Fig. 6 Predicted DRX ratio (XDRX) of S-1.5 + 10-8.5 composite based on Eqs. (1-3) at different temperatures: a 270 ° C, b 320 ° C, c 320 ° C, d 420 ° C |
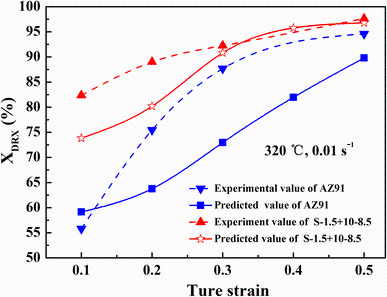
To verify the accuracy of calculated results from thermodynamic analysis, Fig. 7 compares the experimental value with the predicted value of XDRX between AZ91 alloy and S-1.5 + 10-8.5 composite at 320 ° C and 0.01 s-1. With the increase in strain, the experimental value of XDRX rises, which is similar to that of the predicted one in AZ91 alloy and S-1.5 + 10-8.5 composite. Even though some distinction appears between the experimental and predicted value of S-1.5 + 10-8.5 composite at the onset of compression, they are almost identical when the strain exceeds 0.3. Nevertheless, both the experimental and predicted XDRX values of S-1.5 + 10-8.5 composite are higher than that of AZ91 alloy during the whole compression process, which further proves that the existence of SiCp is propitious to enhance XDRX. Moreover, Sect. 3.2 has stated that the addition of SiCp displays obvious effects on reducing the σ c and ε c for DRX. Above analysis and calculation based on compression curves suggest that the existence of SiCp is propitious to stimulate nucleation for DRX. To further verify the DRX behavior based on theoretical analysis, microstructure evolution will be analyzed in the following section.
The as-cast microstructures of S-1.5 + 10-8.5 composite had been given in the previous work [21]. It is demonstrated that both the submicron and micron SiCp were segregated at grain boundaries, exhibiting a typical necklace distribution [21], which was supposed to be resulted from the pushing effect by liquid-solid interface during solidification process [22, 23]. This kind distribution of submicron and micron SiCp is similar to the single-sized 10 μ mSiCp/AZ91 composite in Ref. [24]. It had been widely confirmed that dislocations were easy to pile up at grain boundaries during deformation [25]. Thus, the necklace distribution of SiCp along grain boundaries may have significant effect on the movement of dislocations, which can directly influence the DRX behavior.
To identify the effect of SiCp on microstructure, the optical microstructure of AZ91 alloy and S-1.5 + 10-8.5 composite compressed at 320 ° C and 0.01 s-1 with different strains (0.1, 0.2, 0.3 and 0.5) is given in Fig. 8. It demonstrates that the microstructure of S-1.5 + 10-8.5 composite is absolutely different from that of AZ91 alloy owing to the addition of (submicron + micron) SiCp. Figure 8a shows the microstructure of AZ91 alloy at the strain of 0.1, and it reveals a number of twins near grain boundaries. Only a few fine grains can be found at the junction region of twin boundaries, which indicates the occurrence of DRX. This means that the degree of DRX is very low in the monolithic AZ91 alloy at such low strain. For S-1.5 + 10-8.5 composite at the strain of 0.1, the coarse grains disappear and they are substituted by fine equiaxed grains, which can be identified as the DRXed grains, as shown in Fig. 8b. As compared Fig. 8b to a, the quantity of DRXed grains in S-1.5 + 10-8.5 composite is larger than that in AZ91 alloy. The XDRX of AZ91 alloy and S-1.5 + 10-8.5 composite at 320 ° C and 0.01 s-1 measured by the Image Pro-Plus software is given in Fig. 9a, which demonstrates that the XDRX of S-1.5 + 10-8.5 composite is ~50% larger than that of AZ91 alloy at the strain of 0.1. That means the existence of SiCp is propitious to promote the nucleation for DRX and improve the XDRX of Mg matrix during hot compression process.
 | Fig. 8 Optical microstructures of AZ91 alloy and S-1.5 + 10-8.5 composite compressed at 320 ° C and 0.01 s-1 with different strains (0.1, 0.2, 0.3 and 0.5) |
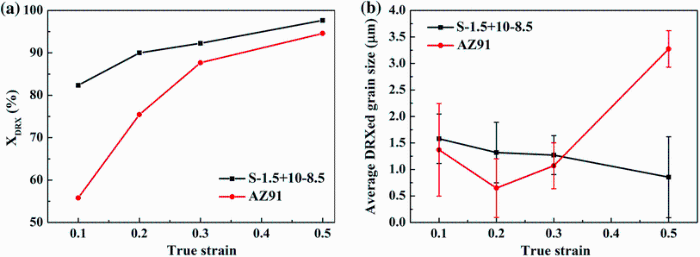 | Fig. 9 XDRXa and average DRXed grain size b of AZ91 alloy and S-1.5 + 10-8.5 composite at 320 ° C and 0.01 s-1 measured by the Image Pro-Plus software |
As the strain increased from 0.1 to 0.5, Fig. 8 shows that the XDRX of AZ91 alloy and S-1.5 + 10-8.5 composite amplifies with the increase in strain. Despite this, variation of the average DRXed grain size in the S-1.5 + 10-8.5 composite remains different from that of AZ91 alloy with the increase in strain, as shown in Fig. 9b. In combination with Figs. 8 and 9b, it can be found that the average DRXed grain size of AZ91 alloy declined as the strain increased from 0.1 to 0.2, and then, it rose as the strain further increased to 0.5. However, the average DRXed grain size of S-1.5 + 10-8.5 composite declined linearly during the whole compression process, which means that the existence of bimodal size SiCp played a significant effect on refining grain size during hot compression process. Figure 8b also manifests that the grains in the vicinity of SiCp are finer than that in particle-free zone, which means the occurrence of DRX is sensitive to SiCp. The SEM microstructure of S-1.5 + 10-8.5 composite at the strain of 0.1 is shown in Fig. 10, which testified the OM observation in Fig. 8b. Besides, nearly no submicron SiCp can be found in the region among micron SiCp; however, many of them distribute at the grain boundaries of fine DRXed grains in Fig. 10b and c. As mentioned above, the submicron and micron SiC particles exhibit a typical necklace distribution along grain boundaries before hot compression. Owing to the weak flow resistance, the submicron SiCp flow easily with Mg matrix during compression process. So the deformation bands consist of a large quantity of submicron SiCp, and fine DRXed grains are formed in Fig. 10b and c. Figure 11 shows the SEM microstructures of S-1.5 + 10-8.5 composite at the strain of 0.2 to 0.5, and it demonstrates that the distribution of submicron SiCp becomes much more uniform with the increase in strain. As compared to the agglomerated submicron SiCp, the particle with uniform distribution can play an effective role in inhibiting grain boundary migration. That is the part reason why the grain size of S-1 + 10-8.5 composite declines as the strain increased from 0.1 to 0.5.
 | Fig. 10 a SEM image of the microstructure of S-1.5 + 10-8.5 composite at the strain of 0.1 (compressed at 320 ° C and 0.01 s-1) and the magnified images of the regions Ab and Bc in Fig. 10a |
The static recrystallization of bimodal size particle-reinforced Al matrix composite had been established, which showed that the recrystallization can be promoted by micron-sized (> 5 μ m) particle; however, the recrystallization kinetics was controlled by fine (< 1 μ m) particles [26]. Therefore, the larger size grains with irregular grain boundaries were obtained after static recrystallization. In the present study, the average grain size of S-1.5 + 10-8.5 composite decreases with the proceeding of compression, which means the DRX behavior of Mg matrix composite is different from the static recrystallization of Al matrix composite, owing to its hcp structure, limit slipping system, low stacking fault energy [27] and high grain boundary diffusion rate [28].
Generally, the DRX process associates with two competing processes: DRXed nucleation and the growth of DRXed grains. So, the average size (d) of DRXed grains depends on its nucleation rate (N) and growth rate (G), which can be described by d = C (G/N)1/4 where C is a constant. Thus, the DRX influenced by bimodal size SiCp depends on its effect on N and G. It is well known that the PDZ with high dislocation density and large orientation gradient can be created by the enforced strain gradient in the vicinity of a non-deformable reinforcement (> 1 μ m), which is thought as an ideal site for the development of a recrystallization nucleus [15]. According to the report of Wang et al. [4], the fine grains are found in the vicinity of 10 μ mSiCp of SiCp/AZ91 magnesium matrix composite. Their following research on the dynamic recrystallization behavior of particle-reinforced Mg matrix composites proves that the formation of PDZ around 10 μ mSiCp promotes the nucleation for DRX [12]. Thus, the existence of micron (10 μ m) SiCp is propitious to DRXed nucleation and improves N value during hot compression process.
Usually, the size of PDZ depends on particle size, which decreases with the decrease in particle size [15]. As the particles size is smaller than 1 μ m, the size of PDZ around them is too small to be considered [13]. Thus, the PDZ’ s effect on DRXed nucleation is weak for submicron SiCp. Despite this, Xu et al. [29] found that the existence of fine Mg17Al12 phase can not only stimulate DRX nucleation by inhibiting dislocation movement, but also refine DRXed grains through the way of pinning grain boundaries. The refined grain size caused by fine particles in Al2O3 nanoparticle-reinforced Mg-based composite has also been given by Habibnejad-Korayem et al. [30]. The dynamic recrystallization behavior of submicron SiCp-reinforced Mg matrix composite had been researched in the previous work [11], which showed that the submicron SiCp can stimulate DRXed nucleation and improve the XDRX through pining dislocations and improving dislocation density around them, which contributed to the fine grain size after hot deformation. At the present study of (0.2 μ m + 10 μ m) bimodal size SiCp-reinforced magnesium matrix composite, the submicron SiCp can also play a significant role in influencing the growth behavior of DRXed grains. As discussed above, the submicron SiCp distribute much more uniformly with the increase in strain, which plays much effective role in inhibiting grain boundary migration. So, existence of submicron SiCp shows obvious effect on reducing G.
Figure 8 and Fig. 9 demonstrate that the DRXed grain size of monolithic AZ91 alloy is fine at the onset of compression, and then, it grows up obviously as the strain is larger than 0.3. That means the G value of AZ91 alloy is low at first, and then, it increases faster than N value with the proceeding of compression. The grain growth behavior seems to play a dominant role for AZ91 alloy, and the average grain size of that is about three times larger than S-1.5 + 10-8.5 composite as the strain increased to 0.5. Softer Mg matrix containing large quantity of harden SiCp indicates the inhomogeneous deformation during hot compression process, which may result in the easy initiation of dislocations. Apart from grain boundaries, SiCp also have pronounced effect on inhibiting dislocation migration and thus lead to the pileup of dislocation around SiCp [16, 31]. The increased dislocations can provide favorable conditions for DRX nucleation [15, 32], so the XDRX of S-1.5 + 10-8.5 composite is higher than monolithic AZ91 alloy during the whole compression process. As compared to monolithic AZ91 alloy, the DRXed grains in the S-1.5 + 10-8.5 composite are hard to grow up during the compression process due to the existence of submicron and micron SiCp. As a consequence, the fine grains are obtained in the S-1.5 + 10-8.5 composite after hot compression.
As a consequence, the S-1.5 + 10-8.5 composite was hot compressed at 270-420 ° C and 0.001-1 s-1. Then, the following conclusion can be drawn based on thermodynamic analysis and microstructure verification:
1. Obvious work softening is found at the flow stress-strain curves of S-1.5 + 10-8.5 composite owing to the occurrence of DRX, which is affected significantly by temperature and strain rate.
2. Both of the critical stress (σ c) and strain (ε c) for DRX are lower than the peak stress and peak strain, respectively. As compared to monolithic AZ91 alloy, the S-1.5 + 10-8.5 composite exhibits lower ε c values at the given strain rate and temperature.
3. The predicted XDRX was consistent with that of experimental value, which increases with the increase in strain. During the whole compression process, the XDRX of S-1.5 + 10-8.5 composite is higher than that of monolithic AZ91 alloy, which indicates the easy occurrence tendency of DRX in bimodal size SiCp-reinforced composite.
4. Microstructure characterization proves that the degree of DRX in S-1.5 + 10-8.5 composite is different from that of monolithic AZ91 alloy. Even though the DRXed grain size in AZ91 alloy is finer than that of S-1.5 + 10-8.5 composite at the initial state, the S-1.5 + 10-8.5 composite possesses the finer grains during the subsequent compression process.
5. Existence of micron SiCp plays a much more obvious effect on promoting DRX nucleation through the formation of PDZ. Distribution of submicron SiCp becomes much more uniform with the increase in strain, which can fully restrain grain growth. Above effects of bimodal size SiCp on Mg matrix contribute to the lower ε c, higher XDRX and fine DRXed grain size of S-1.5 + 10-8.5 composite.
This work was financially supported by the National Natural Science Foundation of China (Nos. 51201112, 51274149 and 51474152), the Natural Science Foundation of Shanxi (No. 2013021013-3) and the Specialized Research Fund for the Doctoral Program of Higher Education (No. 20121402120004).
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|