1 Introduction
Magnesium alloys have increasingly become a viable alternative to iron- and aluminum-based alloys and structural polymers [1]. As a simple ternary alloy system, Mg-Zn-Zr (ZK) is the base alloy of some commercial alloys such as ZE41 and ZE33; ZK61 is one of the successful used wrought magnesium alloys. Recently, Mg-Zn-Y-Zr [2, 3] and Mg-Zn-Gd-Zr [4] have attracted interests for developing high-strength magnesium alloys and Mg-Zn-Ca-Zr [5] alloys for potential biomaterial applications.
Grain refinement is considered to be an effective means of improving as-cast performance of alloys [6]. Introducing heterogeneous nucleation sites and promoting solute growth restriction are two methods for grain refinement of casting magnesium alloys. Zr has been proved to be the most powerful grain refiner for magnesium alloys that do not contain aluminum. However, the addition of Zr is limited, because the solubility of Zr in magnesium is limited and the Zr particles are easy to settle in the melt [7,8,9]. Increasing Zn content could be an alternative to grain refining according to a semiempirical equation which has been proposed to describe the relationship between grain size and solute content [10]:
where mL is the slope of liquidus, k is the solute distribution coefficient and C0 is the solute content of the alloy [14,15,16]. Lee et al. [17] reported the impact of GRF on the grain size of some binary magnesium alloys. The grain size decreases with higher Q value in Mg-Zr [17] and Mg-Zn binary alloys [18]. However, not all cases follow this pattern. Grain coarsening was observed in Mg-Al-Ca alloys [19] with high Q values and similar phenomenon was shown in some Al-Si alloys [20] and Al-Cu alloys [16]. The coarsening mechanisms in those alloys need to be furthure explored.
The grain size is also considered to be related to the dendrite coherency point (DCP), which is defined as the point at which dendrite tips impinge with each other and their neighbors in the entire casting to form a continuous network structure [21]. During solidification, the grain size of the alloy is determined when the DCP is reached. Chai et al. [22] found that both the grain size and the solid fraction at the DCP (fDCPs ) of Al-Cu and Al-Fe alloys decreased with the increase in the solute content. For the Al-Si alloy, with the increase in the solute content, the grain size decreased first and then increased, while the fDCPs value decreased. It indicates that the relationship between grain size and DCP is related to the amount and the type of solute.
Despite the importance of the Mg-Zn-Zr ternary system alloys, surprisingly, only few works investigated the solidification behavior and microstructure formation of Mg-Zn-Zr alloys. Hildebrand et al. [23] investigated the effect of Zn content on the grain size of Mg-xZn-1Zr alloys (x = 0-7 wt%). With increasing the Zn content, the grain size first decreased and reached the minimum at about 4 wt% Zn addition and then increased. They attributed the grain refinement effect to the solubility of Zr in Mg and proposed the formation of Zn-Zr intermetallics decreased the solubility of Zr in Mg and thus refined the grain size of the Mg-Zn-Zr alloys [23]. Cáceres and Blake [24] investigated the grain size and solid solution effects of the Mg-xZn-0.6Zr (x = 0.5-6.9 wt%) alloys. The alloy with 1 at.% Zn had the smallest grain size, but the hardness of the alloys increased with increasing Zn content as a linear relationship. They attributed the strengthening effect in concentrated Mg-Zn alloys to the formation of short-range order (SRO) structure of transitional β’-MgZn2 phase during the solution heat treatment of the alloys.
In this study, we systematically investigate the solidification behavior of Mg-Zn-Zr alloys, including the dendrite coherency point determined by two-thermocouple thermal analysis and Q values from thermodynamic calculations. Furthermore, the effect of grain size on the mechanical properties of Mg-Zn-Zr alloys is investigated. Finally, the possible mechanism of the impact of Zn content on the grain sizes of Mg-Zn-Zr ternary alloys is discussed, providing some fresh ideas for alloy design and grain size prediction of an alloy.
2 Experimental
2.1 Alloy Preparation
Experimental alloys with nominal compositions (wt%) of Mg-0.5Zr (K1), Mg-1Zn-0.5Zr (ZK11), Mg-3Zn-0.5Zr (ZK31), Mg-4Zn-0.5Zr (ZK41) and Mg-5Zn-0.5Zr (ZK51) were prepared in a low-carbon steel crucible heated by a resistance furnace protected by flux. Pure Mg (99.95%) ingots were melted at 700 °C. Then, pure Zn (99.5%) and Mg-30%Zr master alloys were added to the molten Mg at 720-740 °C and 760-780 °C, respectively. After these additions completely melted with stirring, the melt was held at 800 °C for 30 min. Then the temperature was reduced to 750 °C and the melt was poured into a steel mold preheated to 400 °C. A conical ingot with a size of Ф 120 mm × Ф 140 mm × 260 mm was then obtained. The chemical compositions were analyzed using inductively coupled plasma atomic emission spectroscopy (ICP-AES), and the results are listed in Table 1.
Table 1 Chemical compositions of Mg-xZn-0.5Zr (x = 0, 1, 3, 4, 5 wt%) alloys
| Alloys | Zn | Zr | Mg |
|---|---|---|---|
| K1 | 0 | 0.38 | Bal. |
| ZK11 | 0.97 | 0.40 | Bal. |
| ZK31 | 2.82 | 0.50 | Bal. |
| ZK41 | 3.72 | 0.56 | Bal. |
| ZK51 | 4.60 | 0.47 | Bal. |
2.2 Thermal Analysis
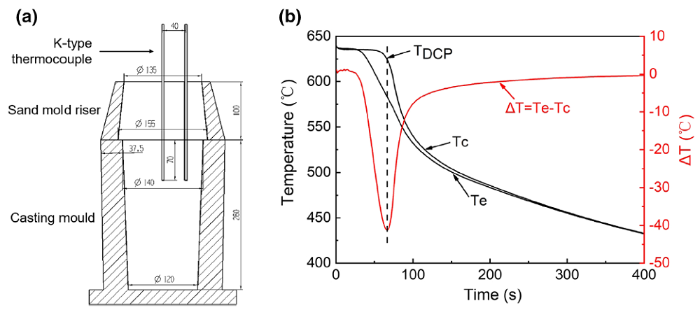
To obtain the DCP of each alloy, thermal analysis was conducted during casting using a pair of K-type thermocouples connected with a DAQ system from the NI Company. As shown in Fig. 1a, the thermocouples were fixed in the center and near the edge of the mold to monitor and record the temperatures of these two positions during the solidification process. The dendrite coherency temperature (TDCP) is obtained as the temperature of the central thermocouple at the largest temperature differences between the central and edge thermocouples, as illustrated in Fig. 1b [21, 25, 26].
Fig. 1
Fig. 1
a Device, b result of thermal analysis for determining the dendrite coherency temperature (TDCP) (Tc and Te refer to the temperatures in the center and near the edge of ingots, respectively)
2.3 Thermodynamic Calculations and Growth Restriction Factors (Q Values)
Thermodynamic calculations, including the phase diagram, solid fractions and growth restriction factors, have been carried out using the integrated software package PANDAT [27] with the PanMg database [28]. The dendrite coherency solid fraction (fDCPs ) is determined through the solid fraction at TDCP on the temperature vs solid fraction curve based on Scheil simulation.
The Q value can be calculated according to Eq. (2) for binary systems, but it is not straightforward for ternary or multicomponent alloy systems, as the mL and k values cannot be obtained directly from phase diagrams. Schmid-Fetzer et al. [29] proposed a method for calculating the Q values of ternary or multivariate alloys using a thermodynamic calculation:
where ΔTcs and fs are the constitutional undercooling of the solid-liquid interface and the solid fraction at the initial stage of the solidification, respectively. Q value represents the developing rate of the supercooled zone at the beginning of grain growth. For an alloy with specific composition, the relationship between ΔTcs (ΔTcs = TL - T, TL refers to the liquidus temperature and T refers to the actual temperature) and fs can be obtained from the Scheil solidification simulation function of the PANDAT software. According to Eq. (3), the Q value is numerically equal to the first partial derivative of ΔTcs to fs as the fs approaches zero.
2.4 Microstructure Characterization
Microstructural observations were conducted using an Axio Observer ZI optical microscope (OM) and scanning electron microscope (SEM, Philips XL30 ESEM-FEG/EDAX). Microanalyses of second-phase compositions were performed by energy-dispersive X-ray spectroscopy (EDAX) attached to the SEM. The samples were cut from the same locations in the ingots and were then ground and polished. Before OM observations, the samples were etched with 4 vol.% nitric acid alcohol solution. The grain sizes were characterized by electron backscattered diffraction (EBSD) images and measured using the linear intercept method. The samples for EBSD were ground to 5000# with SiC abrasive paper and electro-polished with a solution of perchloric acid and alcohol mixture.
2.5 Tensile Test
To investigate the impact of grain sizes on mechanical properties of the alloys, tensile tests were conducted with an AG-100kNG electronic tensile machine from Shimadzu, Japan. The samples were cut from the ingots with gauge lengths of 20 mm and thicknesses of 2.5 mm. Before test, the samples were ground to 2000# with SiC abrasive paper. Three tensile samples were tested at room temperature with an initial strain rate of 1 × 10-3 s-1.
3 Results
3.1 Microstructures
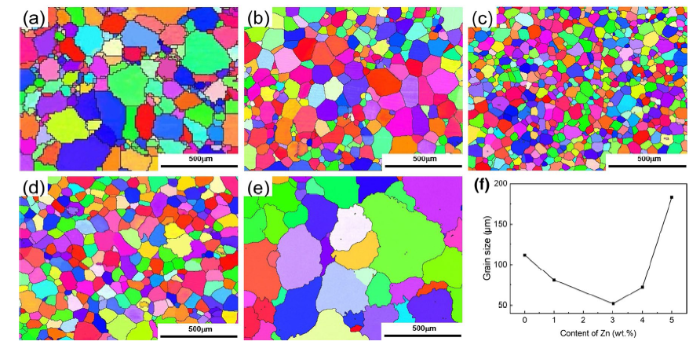
Figure 2 illustrates the optical microstructures of as-cast Mg-xZn-0.5Zr (x = 0, 1, 3, 4, 5 wt%) alloys. First, the morphology of the alloy grains changes with increasing Zn content. The grains change from irregular to regular hexagonal cells when Zn content increase from 0 to 3 wt%. Typical dendritic grains are observed in ZK41 and ZK51 with higher Zn content. Therefore, the alloys can be classified as cell grain alloys with Zn content no more than 3 wt% and dendritic grain alloys for higher-Zn-content alloys. Second, the grain size of the alloys also changes with the addition on Zn. The grain sizes are characterized by EBSD images and determined using the standard linear intercept method, as shown in Fig. 3, and the results are depicted in Fig. 3f. The grain sizes of the alloys first decrease and then increase with the addition of Zn, and the finest grain size is ~ 50 μm in ZK31 alloy.
Fig. 2
Fig. 2
Optical microstructures of a K1, b ZK11, c ZK31, d ZK41, e ZK51 alloys
Fig. 3
Fig. 3
EBSD observations of a K1, b ZK11, c ZK31, d ZK41 e ZK51 alloys, f the detailed grain sizes variation
Figure 4 shows the backscattered electron (BSE) images of the as-cast Mg-xZn-0.5Zr (x = 0, 1, 3, 4, 5 wt%) alloys. Gray α-Mg base and slightly bright halos (indicated by black arrows in the enlarged views in Fig. 4a-c) are observed in K1, ZK11 and ZK31 alloys. Inside and around these halos, a few bright small granules (indicated by white arrows in enlarged views in Fig. 4a-c) are distributed independently or in clusters. The bright halos and dark fields in K1, ZK11 and ZK31 alloys are reported as Zr-rich and Zr-poor areas, respectively. The bright granules are nearly pure Zr particles [8, 30]. In addition to Zr particles, second phases along grain boundaries can be observed in ZK31 (Fig. 4c, d). The amount of second phases increases in ZK41 and ZK51 alloys, as shown in Fig. 4e-h. EDAX analysis indicates that the second phases in ZK31, ZK41 and ZK51 alloys are almost MgZn compounds, and no ZnZr phases are detected.
Fig. 4
Fig. 4
BSE observations of a K1, b ZK11, c, d ZK31, e, f ZK41 g, h ZK51 alloys (the black and white arrows in the enlarged views indicate the Zr-rich areas and Zr particles, respectively)
3.2 Phase Diagram and Scheil Solidification
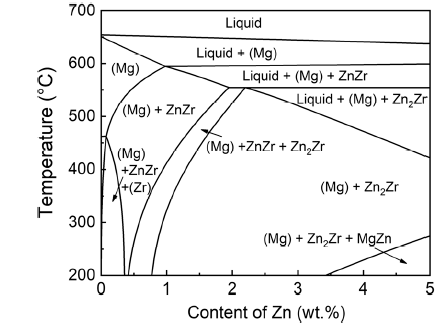
Figure 5 shows the calculated equilibrium phase diagram of Mg-xZn-0.5Zr alloys using PANDAT software with PanMg database (version 2019). With increasing Zn content, some Zn-Zr intermetallic phases (ZnZr or Zn2Zr) form in the alloys after the formation of primary (Mg) phase. In all alloys, (Mg) phase is always the primary phase, and no Zn-Zr intermetallic phases precipitate before (Mg) phase to act as heterogeneous nucleation sites for primary (Mg) phase.
Fig. 5
Fig. 5
Thermodynamic calculated phase diagram of Mg-xZn-0.5Zr alloys
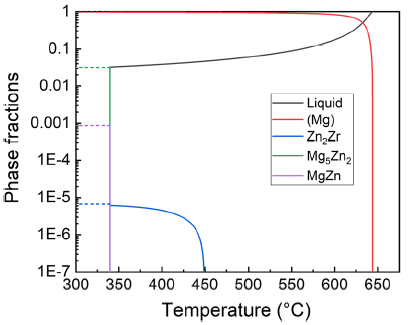
Figure 6 represents the mole fraction of different phases during Scheil solidification of ZK31 alloy. The result indicates that (Mg) phase solidified as primary phase, Zn2Zr phase precipitates at 449 °C and solidification ends at 340 °C with the eutectic of (Mg) + Mg5Zn2 + MgZn. As the phase fraction of Zn2Zr phase is less than 1E - 5, it is difficult to be detected in SEM as shown in Fig. 4.
Fig. 6
Fig. 6
Phase fraction evolution of ZK31 alloy during solidification with Scheil simulation
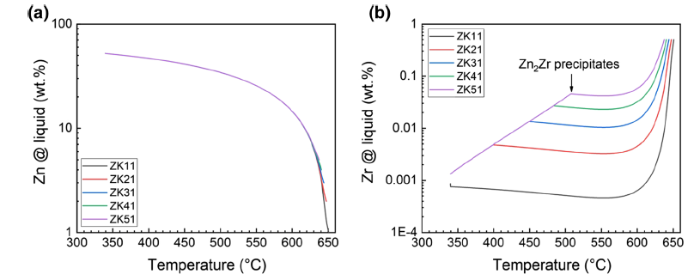
Figure 7 shows the solute content in the remaining liquid phase during solidification of the Mg-xZn-0.5Zr under Scheil simulation. During Scheil solidification, Zn is enriched in the liquid phase. The initial content of Zn in different alloys is different, but the Zn content in the remaining liquid phase is close to the same value at temperature lower than 610 °C as shown in Fig. 7a. On the other hand, as Mg-Zr is peritectic reaction at Mg-rich corner, the Zr content in the remaining liquid phase decreases during solidification, and the decline becomes even more rapidly after starts precipitating Zn-Zr compounds, as indicated in Fig. 7b.
Fig. 7
Fig. 7
a Zn content, b Zr content in the remaining liquid phase during Scheil simulation
3.3 Growth Restriction Factors (Q Values)
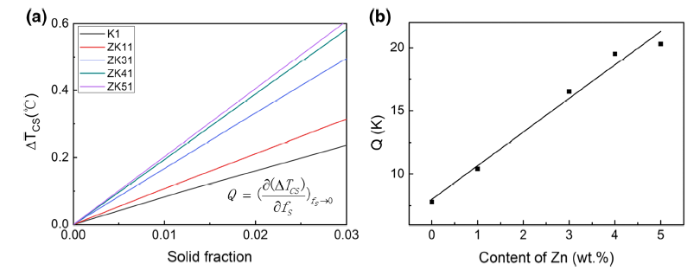
Figure 8a shows the relationship between the calculated ∆Tcs (∆Tcs = TL - T) and the fs of Mg-xZn-0.5Zr (x = 0, 1, 3, 4, 5 wt%) alloys at a low solid fraction range. The constitutional undercooling (∆Tcs) of each alloy contributed by Zr can be considered the same, because no ZnZr compound precipitates at the beginning of the solidification as shown in Fig. 5. Therefore, the different ∆Tcs of each alloy attributes to the change of Zn addition. According to Eq. (3), Q values are determined by the slope of the lines in Fig. 8a. The Q values calculated are almost proportional to the solute contents as shown in Fig. 8b, which is consistent with Eq. (2). The slight deviation between the calculated Q values and the fitting line is because the slope of liquidus (mL) and the solute distribution coefficient (k) for each alloy are slightly different.
Fig. 8
Fig. 8
a Plots of the constitutional undercooling against solid-phase fraction of Mg-xZn-0.5Zr (x = 0, 1, 3, 4, 5 wt%) alloys at the initial stage of solidification ,b the calculated Q values variation against Zn content
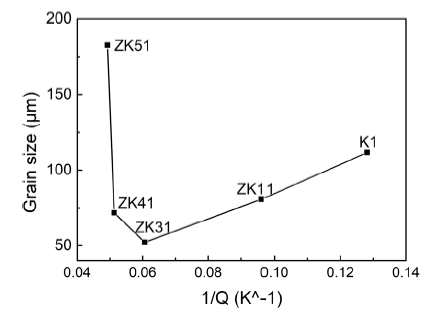
The influence of the solute content on the grain size is traditionally determined by the Q value [10, 31]. According to Eq. (1), grain size of an alloy is linearly positively correlated with 1/Q, which agrees well with the result in this study when the content of Zn is no more than 3 wt% as shown in Fig. 9. However, when the content of Zn is more than 3 wt%, the grain sizes increase with the decrease in 1/Q (or the increase in Q). A similar phenomenon was also found in other alloy systems such as Al-Si [20], Al-Cu [16] and Mg-Al-Ca [19] alloys. This indicates that the GRF theory can only be applied within certain solute content limits. In other words, the solute content should not exceed a critical value for a specific alloy system when the Q value is used to predict grain sizes. The critical solute content was about 5.5 wt% Cu in Al-Cu alloys [16] and 3 wt% Si in Al-Si alloys [20]. In this study, the critical content of Zn is 3 wt%. The phenomenon of grain coarsening in ZK41 and ZK51 alloys cannot be explained by GRF theory alone.
Fig. 9
Fig. 9
Plot of the measured grain size against 1/Q of Mg-xZn-0.5Zr (x = 0, 1, 3, 4, 5 wt%) alloys
3.4 Dendrite Coherency Parameters
With the thermal analysis, the DCP is determined by the minimum point of the ΔT curve as shown in Fig. 1b. According to the concept of DCP, a channel for heat conduction is formed with the establishment of a dendritic network at this point. The temperature difference between the edge and the central areas will reach a maximum value at this point because of a considerable difference in thermal conductivity between the liquid and solid phases [21]. Accordingly, the corresponding dendrite coherency temperatures (TDCP) of Mg-xZn-0.5Zr (x = 0, 1, 3, 4, 5 wt%) alloys are obtained and listed in Table 2.
Table 2 Dendrite coherency temperatures of Mg-xZn-0.5Zr (x = 0, 1, 3, 4, 5 wt%) alloys
| Alloys | K1 | ZK11 | ZK31 | ZK41 | ZK51 |
|---|---|---|---|---|---|
| TDCP (°C) | 650 | 645 | 636 | 626 | 630 |
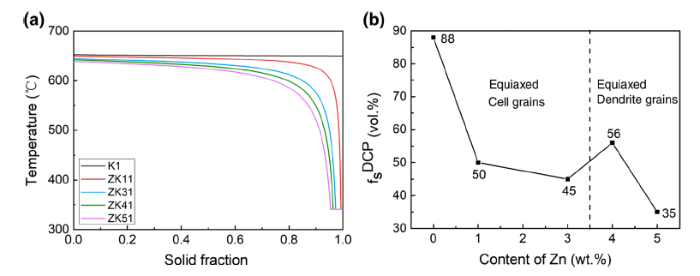
Figure 10a depicts the plots of temperature (T) against solid fraction (fs) calculated by the Scheil simulation using PANDAT. In the T - fs curve, the solid fraction corresponding to the dendrite coherency temperature (TDCP) is the dendrite coherency solid fraction (fDCPs ). Accordingly, Fig. 10b shows the fDCPs values of Mg-xZn-0.5Zr (x = 0, 1, 3, 4, 5 wt%) alloys and their variation trend with Zn additions. As can be seen, the fDCPs values decrease with increasing Zn content except a small peak at 4 wt% Zn. This is strongly related to the grain size and grain morphology, because the DCP marks the transition from mass feeding to interdendritic feeding, and after the DCP reaches, the grains grow in the form of dendrite thickening [21]. Therefore, the fDCPs values are also used to explain the grain size variation, which is discussed in detail below.
Fig. 10
Fig. 10
a Plots of temperature against solid fraction of Mg-xZn-0.5Zr (x = 0, 1, 3, 4, 5 wt%) alloys calculated by the Scheil simulation, b dendrite coherency solid fractions (fDCPs ) of the alloys obtained from (a)
3.5 Mechanical Properties
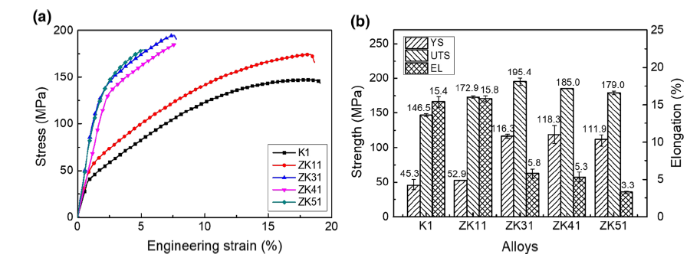
Grain size can strongly affect the mechanical properties. Figure 11 shows the typical engineering stress-strain curves of the as-cast Mg-xZn-0.5Zr (x = 0, 1, 3, 4, 5) alloys and the detailed tensile properties. According to the mechanical properties, these five alloys can be classified into two groups. The K1 and ZK11 alloys are classified into Group I, which possess high ductility but poor strength. ZK31, ZK41 and ZK51 are classified into Group II, which has lower ductility but higher strength than the alloys in Group I.
Fig. 11
Fig. 11
a Stress-strain curves, b detailed properties of as-cast Mg-xZn-0.5Zr (x = 0, 1, 3, 4, 5) alloys
The obvious difference between Groups I and II in terms of microstructure is the formation of the MgZn intermetallic phase. The effect of MgZn intermetallic phase on the mechanical properties in Mg-Zn alloys is similar to that of Al12Mg17 in Mg-Al alloys, but the strengthening effect of the MgZn phase in Mg-Zn alloys is more significant. The hard brittle MgZn phase distributed along the grain boundaries can pin the grain boundaries and impede the movement of dislocations, thereby improving the yield strength [32]. However, the MgZn phase is prone to promote cracks and deteriorate the ductility. Within Group I, there is little second phase (Fig. 4a, b). The higher strength in ZK11 alloy than that in K1 alloy is mainly due to the solution strengthening effect of Zn. In Group II, a fraction of the MgZn phases increase with increasing the addition of Zn (Fig. 4c-h). The ZK31 alloy exhibits the best combined properties with yield strength (YS) of 116.3 MPa, ultimate tensile strength (UTS) of 195.4 MPa and elongation (EL) of 5.8%. The best combined mechanical properties of the ZK31 alloy can be attributed to the finest grain size and homogenously distributed small intermetallic strengthening phases, as shown in Figs. 3c and 4c.
Refined grains serve to enhance yield strength based on the Hall-Petch relationship:
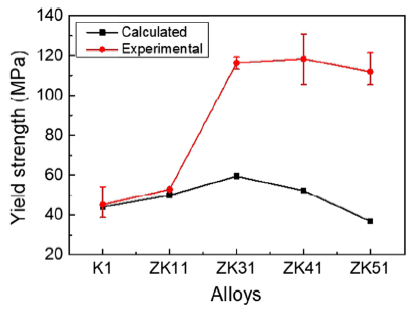
where \(\sigma\) is the yield strength, \(\sigma_{0}\) is the friction stress of the dislocation glide on the slip plan, ky is the Hall-Petch coefficient and d is the grain size [33]. The values of \(\sigma_{0}\) and ky for quenched Mg-Zn alloys have been summarized by Robson and, respectively, are 11 MPa and 0.35 MPa m1/2 [34]. Figure 12 compares the calculated yield strength according to Eq. (4) with the tensile yield strength measured experimentally. As can be seen, the smallest grain size does contribute to the greatest strength increase for ZK31. In contrast, the coarsest grains lead to the least strength increase for ZK51. For the alloys in Group I, the yield strength is almost entirely contributed by grain size. However, for Group II, the yield strength of the three alloys is much higher than that contributed by grain size. As analyzed above, the secondary phases also contribute to the improvement on strength. Although there are a large number of second phases in ZK51 (Fig. 4g, h), the poor properties caused by grain coarsening cannot be completely compensated.
Fig. 12
Fig. 12
Tensile yield strength experimentally measured and the yield strength contributed by grain size based on the Hall-Petch equation
4 Discussion
As shown in Fig. 3, the grain sizes of as-cast Mg-xZn-0.5Zr alloys decrease first and then increase with the addition of Zn. The finest grains are obtained in the alloy with 3 wt% Zn, and this takes major responsibility for the best comprehensive mechanical properties of ZK31. Actually, similar results were also reported by Hildebrand et al. [23] and Cáceres and Blake [24]. The grain size first decreased and then increased with increasing the content of Zn in Mg-xZn-Zr alloys. Their Mg-xZn-1Zr alloys showed finest grain size alloy located between 3 and 4 wt% Zn. On the other hand, the grain size of Mg-xZn alloy decreased gradually with increasing Zn content up to 6 wt% [18]. Hildebrand et al. [23] attributed the grain refinement effect to the solubility of Zr in Mg and proposed the formation of Zn-Zr intermetallics decreased the solubility of Zr in Mg and thus refined the grain size of the Mg-Zn-Zr alloys with higher Zn content [23]. However, based on the present thermodynamic calculations, as shown in Fig. 7b, the formation of Zn-Zr intermetallic phases decreases the concentration of Zr in the remaining liquid phase, but it occurs at temperature much lower than the liquidus temperature. These temperatures are even lower than the TDCP as shown in Table 2. Therefore, the formation of Zn-Zr compounds should have limited impact on the grain size of the alloys.
Another feature observed in the present work is the grain morphologies change with the additions of Zn. When Zn content is higher than 3 wt%, the alloy grains change from cell grains to dendritic grains. According to the basic theory of solidification [35], the solute content has two effects on the grain growth due to the constitutional undercooling caused by solute enrichment at the solid-liquid (S - L) interface. First, a modest constitutional undercooling provides a necessary condition for nucleation and encourages the embryos to grow into stable nuclei, and it decreases grain growth rate because of the difficult diffusion of solutes as the temperature drops. This tends to refine grains. Second, a large constitutional undercooling can lead to the instability of the S - L interface which prompts grains to transform from columnar to dendritic. The sharp tip of the dendrite increases the growth rate of the dendritic grains and thus leads to coarser grains.
The first effect is dominant when the solute content is low. In this study, when the Zn addition is no greater than 3 wt%, the diffusion of solutes controls the growth of grains, and the inhibitory effect of solute enrichment on grain growth enhances with the increase in the Zn content. The inhibiting effect of solute atoms on the grain growth is usually measured by the Q value. According to Eq. (3), a larger Q value indicates a higher initial rate of development of constitutional undercooling [15, 31]. In other words, the undercooled zone at the front of the growing grain is easier to form for an alloy with a large Q value, which encourages the formation of embryos and stable nuclei. On the other hand, the inhibiting effect of solute content on grain growth rate can be given as follows [22, 36]:
where V is the grain growth rate, A is a constant, DL is the liquid diffusion coefficient, Γ is the Gibbs-Thomson parameter, m is the slope of the liquidus line, C0 is the original solute concentration, k is the solute distribution coefficient and ΔT is the undercooling of the melt at the dendrite tip. It is justified to neglect the thermal undercooling for equiaxed solidification [14]. As can be seen, assuming that the DL, ΔT and Γ are constants, the grain growth rate is inversely proportional to Q value (\(mC_{0} (k - 1)\)). Therefore, a larger Q value indicates a lower growth rate, which resulted from the restriction effect of solute enrichment. Therefore, in this study, the GRF theory can be applied to explain the grain sizes of the alloys with Zn addition is no greater than 3 wt%. For K1, ZK11 and ZK31 alloys, the grains grow as cell grains in all directions. The grain size decreases with the higher solute content as shown in Fig. 3, and the curve of grain sizes against 1/Q shows good linear relationship of Eq. (1) in Fig. 9.
The second effect becomes dominant when the solute content is further increased to produce enough undercooling. In this study, the grains become dendritic in ZK41 and ZK51, as shown in Fig. 2. In this case, the undercooling is heavily affected by the curvature radius of dendrite tips. In fact, the undercooling ΔT in Eq. (5) is the sum of thermal undercooling ΔTt, constitutional undercooling ΔTc and curvature undercooling ΔTr. The ΔTr can be given as follows [35]:
where Γ is the Gibbs-Thomson parameter and r is the curvature radius of dendrite tip. Smaller r in the dendrite tip leads to larger ΔTr and then larger ΔT. When the effect of solutes on ΔTr is greater than Q, a small r will lead to a large growth rate and finally large grains [22]. Therefore, the grain size of ZK51 is larger than that of ZK41 due to the more developed dendritic structure of ZK51 alloy. A similar grain coarsening effect of solute element due to the formation of developed dendritic structure was also reported in Mg-Al-Ca alloys [19]. Meanwhile, a large growth rate tends to make the dendrites become coherent earlier. After the DCP reaches, the grains grow mainly in the form of dendrite thickening [21]. Therefore, a lower dendrite coherency solid fraction (fDCPs ) and a larger grain size are obtained in ZK51 than that in ZK41.
Both the grain sizes and the fDCPs values decrease with the increase in the Zn content in K1, ZK11 and ZK31 alloys. This is because the three alloys have low solute contents, and the grains grow in the form of equiaxed crystals as shown in Fig. 2. The effect of solute enrichment on grain growth is much more significant than that of grain morphology. According to Eq. (3) of the GRF theory, a lower solute content means a slower formation rate of the undercooled zone in the initial solidification stage, which tends to make the nuclei fewer. The grains must consume more liquid to impinge with each other. In other words, the DCP is not reached until the corresponding solid fraction is high. Therefore, the fDCPs values decrease in K1, ZK11 and ZK31 alloys. What is more, a smaller grain size corresponds to a shorter distance between grains, which tends to make the dendrites become coherent earlier [22], and then, the fDCPs value will be lower. This is also responsible for the skip of fDCPs value from 45 vol% for ZK31 to 56 vol% for ZK41 as shown in Fig. 10b.
According to the above analysis, the GRF theory is not applicable in all cases, but there exists a critical Q value (or a critical solute content). When the solute content exceeds the critical value, more factors should be considered to predict grain size variation. In this study, the dendrite morphologies strongly affect the final grain size when the Zn content exceeds 3 wt%. Considering both the GRF and DCP theories, the “abnormal phenomenon” of the increase in grain sizes with the increase in Q values could be explained reasonably. It should be noted that more factors may need to be included for other alloys or more complex. The solidification process involves complex kinetics and thermodynamics, and this study simply focuses on the solidification process from the perspective of thermodynamics.
5 Conclusions
In this study, the solidification behavior and microstructure formation of the Mg-Zn-Zr alloys have been extensively investigated. The grain refining and coarsening mechanisms have been discussed from the perspective of growth restriction factor (GRF) and dendritic coherency point (DCP). The following conclusions are achieved:
1. The grain size of Mg-xZn-0.5Zr (x = 0, 1, 3, 4, 5 wt%) alloys first decreased and then increased with increasing Zn content. The finest grains were obtained in the alloy with 3 wt% Zn addition, and this is a major reason for the best comprehensive properties of ZK31 alloy compared to the other alloys.
2. Thermodynamic calculations show that the Zn-Zr compounds precipitate after the primary (Mg) phase during solidification, and thus may have little impact on the grain size of the alloys.
3. Both the GRF and DCP which are related to solute content should be considered to predict the grain size in this study. The GRF theory is applied for the grain refinement effect in K1, ZK11 and ZK31 alloys. The morphology change based on DCP theory may be responsible for the grain coarsening effect in ZK41 and ZK51 alloys.
The growth restriction factor (Q) and dendrite coherency solid fraction (fDCPs ) are strongly associated with solidification process. The investigation on the relationship between Q, fDCPs and grain size may provide some thermodynamic data for alloy design and grain size prediction. However, more studies on these parameters are needed to help to further understand the mechanisms of grain refinement and grain coarsening related to solute content.
Acknowledgements
Z.W. Shan and his students acknowledge the supports by the National Key Research and Development Program of China (No. 2017YFB0702001) and the Natrual Science Foundation of China (No. 51621063). They also appreciate the support from the International Joint Laboratory for Micro/Nano Manufacturing and Measurement Technologies, the Collaborative Innovation Center of High-End Manufacturing Equipment and the Science and Technology Department of Shaanxi Province (Nos. 2016KTZDGY-04-03 and 2016KTZDGY-04-04). R.S. Chen and his students acknowledge the National Natural Science Foundation for Young Scholars (No. 51701218) and the National Science and Technology Major Project of China through Project No. 2017ZX04014001.
Reference
The Interdependence Theory links grain formation and nucleant selection to improve the ability to reveal the mechanisms of grain refinement, predict as-cast grain size and account for observations that only a small proportion of added inoculant particles nucleate grains. The Interdependence Theory addresses these issues from a different fundamental perspective, which assumes that grain formation is the result of the interdependence between nucleation and growth acting in concert within an environment dictated by the alloy chemistry. The final grain size is determined by three components: (i) the distance that a previously nucleated grain must grow in order to establish sufficient constitutional supercooling (CS) ahead of a solid liquid (S L) interface to enable nucleation of the next grain; (ii) the distance from this S L interface to the point where this critical amount of CS has been generated; and (iii) the additional distance to the nearest most potent nucleant particle. The first and second components together represent a nucleation-free zone where nucleation is completely suppressed. The relative significance of each component is assessed using experimental data on magnesium and aluminium alloys. To improve particle efficacy and promote nucleation and grain refinement it is critical to minimize the size of the nucleation-free zone by controlling alloy chemistry and/or growth rate. The Interdependence Theory clearly explains why only a small proportion of added inoculants particles are operative. (C) 2011 Acta Materialia Inc. Published by Elsevier Ltd.
AbstractBeing able to predict the grain formation process and attendant grain size has been a central topic in solidification. Such an analytical model is presented for constitutional supercooling (CS)-driven grain formation with several simplifications. The model links the nucleation of new grains to the growth of a larger neighbouring grain. The average grain size () is thus determined by two components: the minimum growth (rcs) necessary to establish sufficient CS (ΔTn) for nucleating new grains, and the spatial mean distance () to the most potent available nucleants. Both spherical and planar growth fronts are considered, covering growth curvatures from small to infinite. Two distinct fundamental approaches are used, which result in identical descriptions of , where (D is the diffusion coefficient, v is the growth velocity, Q is the growth restriction factor). The model is compared with literature data produced under various conditions and demonstrated on aluminium alloys as an example.]]>
AbstractThe amount and type of alloying elements in aluminium affect the as-cast microstructure through the dependence of solidified fraction on undercooling. This can be quantified by the growth-restriction parameter Q. Phase-diagram calculations using the CALPHAD method show the effects of thermodynamic parameters on Q. In binary systems, the deviation from linear dependence of Q on solute concentration is assessed. In ternary alloys, model systems elucidate the role of solute interaction in the liquid and solid, and can be used to interpret the behaviour in actual systems. Growth restriction is discussed in relation to solidification modelling and the attainment of a fine, equiaxed microstructure in wrought and shape-casting alloys.]]>
AbstractThe newly enhanced PANDAT, integrating PanEngine, PanOptimizer and PanPrecipitation, bridges thermodynamic calculation, property optimization, and kinetic simulation of multi-component systems based on CALPHAD (CALculation of PHAse Diagram) approach. This software package, in combination with thermodynamic/kinetic/thermo-physical databases, provides an integrated workspace for phase diagram calculation and materials property simulation of multi-component systems. The simulation results, which include thermodynamic, kinetic, thermo-physical properties, and microstructure related information, are critically needed in materials design, in the selection of parameters for fabrication steps such as heat treatment, prediction of performance, and failure analysis. In addition to the functionalities provided by PANDAT as a stand-alone program, its calculation/optimization engines (PanEngine, PanOptimizer and PanPrecipitation) are built as shared libraries and enable their integration with broader applications in the field of Materials Science and Engineering.]]>
The growth restriction factor Q is the key quantity in current descriptions of the solutal effect on grain growth and grain refinement during solidification of alloys. A rigorous treatment for the evaluation of Q in multicomponent alloys based on consistent thermodynamic descriptions of the alloy phase equilibria is presented. On closer inspection the conventional approach to calculate Q in multicomponent alloys from liquidus gradient m(i) and partition coefficient k(i) must fail for a wide range of common alloys exhibiting minute amounts of primary crystallizing intermetallic phase, exemplified for Mg-Al-Mn and Al-Si-Ti alloys. The rigorous approach provides an extension of the applicability range of the concept of Q. The qualitative similarity of inoculant particles and primary intermetallic phases is verified by calculations for Al-Si-Ti-B alloys. (C) 2011 Acta Materialia Inc. Published by Elsevier Ltd.
AbstractA model for the determination of relative grain size is developed based on the assumption that nucleant substrates are activated by constitutional undercooling generated by growth of an adjacent grain. The initial rate of development of constitutional undercooling is shown to be equivalent to the growth restriction factor and is a useful approximation for the effect of solute on grain size when potent nucleant substrates are present. However, when the nucleants are of a poor potency then a calculation of the fraction solid necessary to develop the constitutional undercooling required for nucleation needs to be performed. Using the model, trends in grain size observed experimentally by the addition of titanium to pure aluminium and to a typical casting alloy, AlSi7Mg0.3, can be predicted. It was also found that summing the individual growth restriction factors of each solute element in a multi-component alloy can grossly overestimate the actual value of the growth restriction factor for the alloy.]]>






 WeChat
WeChat
