Titanium alloys have been extensively used in aircraft engine blade and blisk due to their high specific strength, good fracture toughness and preeminent high-temperature performance [1,2,3,4,5]. The excellent service performance of titanium alloys is not only related to the chemical composition, but also to the various microstructures [6,7]. Due to allotropic transformation, the titanium alloys generally possess α + β dual-phase microstructure. The α phase has three typical geometric morphologies, including equiaxed, lamellar and dispersed, and the morphology has a significant effect on the strength and toughness of titanium alloys [8,9,10,11,12]. To optimize the microstructural parameters and service performance, it is necessary to study the deformation mechanism to reveal the influence of microstructure on mechanical properties and then provide a theoretical foundation for microstructure design.

The deformation mechanism of α and β phases is closely related to the chemical composition in titanium alloy [13,14,15,16,17]. During deformation at room temperature, both slip and twinning could occur in α phase in pure titanium [18,19,20,21], and slip, twinning, and stress-induced martensitic transformation could occur in β phase in β titanium alloys [22,23,24]. According to the Von Mises criterion [25], for homogeneous plastic deformation, it requires at least five active and independent slip systems. However, for α phase, extensive investigations have shown that easily initiated < a > basal and < a > prismatic slip only enable a maximum of four independent slip systems [26,27]. Therefore, additional plasticity mechanisms to coordinate deformation are indispensable, including < c + a > pyramidal slip and twinning [26]. Typically, in pure titanium, twinning is more easily initiated to coordinate deformation than < c + a > pyramidal slip [28]. However, for most near-α and α + β titanium alloys, with the increase in aluminum and oxygen contents in the alloy, twinning is suppressed in α phase [15,28], such as Ti-5Al-2.5Sn [29], Ti-6Al-4V [30] and Ti-8Al-1Mo-1V [31] alloys. As a result, further coordinated deformation of these alloys is dependent on < c + a > pyramidal slip and β phase with abundant slip systems [28,32], and then, slip would dominate plastic deformation of α phase [2,33,34].

Generally, slip initiation and slip transfer behavior not only have a significant effect on the yield strength, but also are closely related to crack nucleation of titanium alloys [33,35]. It has been shown that titanium alloys with easily initiated slip have a relatively low yield strength [36], and more slip transfer behavior between adjacent grains could effectively coordinate deformation and then increase the plasticity of the alloy [32]. In addition, the formation of crack could often reduce plasticity and fatigue strength [32,37]. Therefore, investigating the slip initiation mechanism in the grain, and slip transfer mechanism across the grain/phase boundaries during deformation, is crucial to reveal the microstructure-property relationship for optimizing the mechanical properties of titanium alloys.

Recently, the deformation mechanism of titanium alloys could be investigated by in situ X-ray diffraction (XRD), in situ transmission electron microscopy (TEM) and in situ scanning electron microscopy-electron backscattered diffraction (SEM-EBSD) techniques. However, the three above techniques present different advantages for studying deformation mechanism. The in situ XRD technique could be adapted to study the lattice strain and stress tensor generated in individual grains during deformation [38,39]. The in situ TEM technology is suitable for the study of dislocation nucleation mechanism and dislocation movement due to its ability to directly observe the evolution of dislocation morphology [40,41,42]. The in situ SEM-EBSD technique is utilized to study the slip behavior by combining crystallographic information with the morphology of slip trace generated during deformation [43,44]. Comparing with the in situ XRD and in situ TEM techniques, the in situ SEM-EBSD technique exhibits the advantage of simultaneously obtaining the information of deformation mechanism and mechanical properties due to the relatively large size of the experimental specimen [45,46]. Therefore, the relationship between deformation mechanism and mechanical behavior could be effectively established through the application of in situ SEM-EBSD technique.

Based on the previous studies of deformation mechanism in near-α and α + β titanium alloys, this paper reviewed and discussed the slip initiation, slip transfer and crack nucleation mechanism. It could be beneficial to revealing the influence of microstructure on the mechanical properties and providing the guidance for further study on deformation mechanism of titanium alloy.

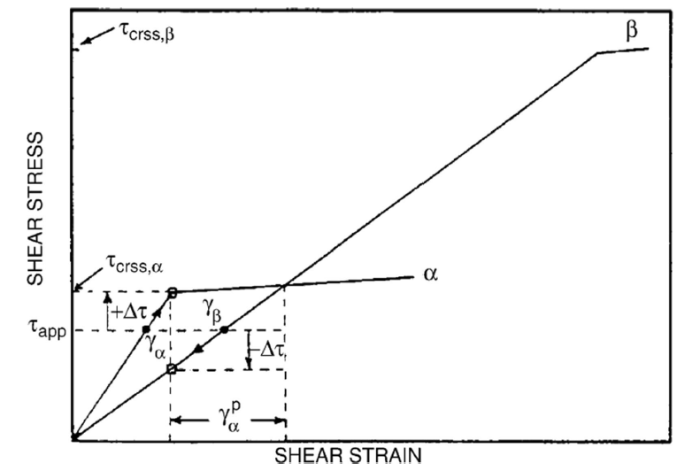
In dual-phase titanium alloys, both α and β phases could experience plastic deformation. However, the slip initiation between α and β phases is asynchronous during deformation, which is mainly related to the different strength and elastic modulus of the two phases. In general, at the micron scale, the elastic modulus of α phase is higher than that of β phase [47,48], and the strength of β phase is higher than that of soft α phase [49,50]. Additionally, the hardness of β phase is about three times that of α phase [51]. Due to the difference in the strength and elastic modulus between α and β phases, an interaction stress would be generated between the two phases during deformation, which could affect the actual stress state of α and β phases. Ankem et al. [52] found that, under a given applied stress, the α phase experienced less elastic strain than β phase during early deformation due to the higher elastic modulus of α phase than β phase. However, to maintain strain compatibility, the strains in α and β phases are forced to coincide. Consequently, the interaction stress is generated between the two phases, which would result in the increment of stress in α phase and deduction of stress in β phase. As shown in Fig. 1 [52], under the combined effect of the interaction stress (∆τ) and applied stress (τ_app), the actual stress in α phase is τ_app + ∆τ, and the actual stress in β phase is τ_app-∆τ. Meanwhile, according to the finite element calculation, it was found that the actual stress in α phase was larger than β phase near the α/β interface [53]. As a result, slip is usually initiated preferentially in α phase during deformation because of its higher actual stress and lower strength than β phase.

Recently, many researchers have investigated the sequence of slip initiation between α and β phases through in situ experiments. By in situ TEM, Castany et al. [54] investigated the slip behavior of Ti-6Al-4V alloy with lamellar structure during tensile deformation and observed that the dislocation loops forming at α/β interface firstly moved into α phase, indicating that the slip was preferentially initiated in α phase, as shown in Fig. 2. Zhou et al. [32] found that, in the fully equiaxed microstructure of TA19 titanium alloy, the slip trace was generated in equiaxed α grain prior to intergranular β phase, indicating the preferential slip initiation in equiaxed α phase (Fig. 3a). Similarly, Suri et al. [55] reported that, in an α colony consisting of parallel α and β lamellae, the slip trace firstly appeared in α phase and then cross the α/β interface into β phase with the increase in strain, suggesting that slip initiation in β phase depended on the slip transfer behavior from α to β phase.

However, Wang et al. [48] found that some slip traces just appeared in the interlayer β phases of full lamellar microstructure (as shown in Fig. 3b), indicating that the slip could be also preferentially initiated in β phase within an α colony. It is mainly related to the interaction stress between different colonies. It is well known that the Young's modulus of α phase decreases with the increase of θ (the angle between the c-axis and the applied stress axis) [56,57,58]. During deformation, elastic deformation could be easily aroused in α colony with low Young's modulus. To maintain strain compatibility, neighboring α colony with high Young's modulus experienced the preferential plastic deformation after a small elastic deformation, which could coordinate the elastic deformation of α colony with low Young's modulus. Thus, at a certain strain, the strong internal stress could be caused by the inhomogeneous deformation of adjacent α colonies with different Young's modulus. It would change the stress state of α and β phases and promote the slip initiation in the interlayer β phase of an α colony with low Young's modulus [48].

The hexagonal close-packed α phase has <a> basal $\{ 0001\} {<}11\overline{2}0 {>}$, < a > prismatic $\{ 10\overline{1}0\} {<}11\overline{2}0 {>}$, < a > pyramidal $\{ 10\overline{1}1\} {<}11\overline{2}0 {>}$ and < c + a > pyramidal $\{ 10\overline{1}1\} {<}11\overline{2}3 {>}$ slip systems, and their slip initiation depends on the critical resolved shear stress (CRSS) and Schmid factor (SF) [59,60,61,62]. During deformation, the slip system can only be initiated when the resolved shear stress (RSS) exceeds the CRSS. The RSS on a given slip system is $\tau = \sigma \cos \lambda \cos \phi = \sigma m$ [63], where $\tau$ is the RSS, $\sigma$ is the applied stress, $\lambda$ is the angle between the applied stress direction and slip direction, and $\phi$ is the angle between the applied stress direction and normal direction of slip plane, and $m = \cos \lambda \cos \phi$ is the SF [64]. The larger $m$ value leads to the larger RSS of the slip system, which would benefit the slip initiation. Therefore, slip system with high SF and low CRSS is easily initiated during deformation.

At room temperature, the CRSS of prismatic slip in pure titanium is generally much lower than that of other slip modes, and the CRSS of basal slip is lower than that of pyramidal slip [38,65,66,67]. However, the content of alloy elements (especially the Al element) has a significant effect on the CRSS [15,68] and slip initiation behavior. It has been shown that increasing the Al content would lead to an increase in the c/a ratio of α phase [69,70,71] and a decrease in the stacking fault energy on the basal plane [72,73], which would change the prismatic/basal CRSS ratios. For different titanium alloys of CP-Ti, Ti-5Al-2.5Sn and Ti-6Al-4V, the prismatic/basal CRSS ratios were 0.28, 0.81 and 1.2 at the similar strain of 4%, respectively [69]. It is apparent that the prismatic/basal CRSS ratio increases with the increase of Al content, which could promote the initiation of basal slip in α phase. Mine et al. [70] reported that the CRSS of < a > basal slip ($(0001)[2\overline{1}\overline{1}0]$), < a > prismatic slip ($(0\overline{1}10)[2\overline{1}\overline{1}0]$) and < c + a > pyramidal slip ($(01\overline{1}1)[\overline{1}\overline{1}23]$) in Ti-6Al-4V was 330 MPa, 410 MPa and 690 MPa, respectively, indicating that basal slip could be easily initiated in Al-rich titanium alloy.

The addition of vanadium (0.134 nm) and molybdenum (0.139 nm) elements has a weak effect on the CRSS and slip initiation [74], because the two elements have the similar atomic radii to titanium (0.147 nm) and could not effectively change the c/a ratio of α phase [74]. Hémery et al. [75] found that molybdenum content, compared with Al content, had a limited effect on the prismatic/basal CRSS ratios in Ti-6Al-2Sn-4Zr-xMo (x = 2, 6) alloy. Barkia et al. [76] investigated the effect of oxygen content on the deformation mechanism of pure titanium and found that the increase in oxygen content (1600 ppm → 3200 ppm) increased the CRSS of slip systems, but had little effect on the prismatic/basal CRSS ratios. Therefore, a competition of slip initiation between basal and prismatic slip systems during deformation is not sensitive to the vanadium, molybdenum and oxygen content.

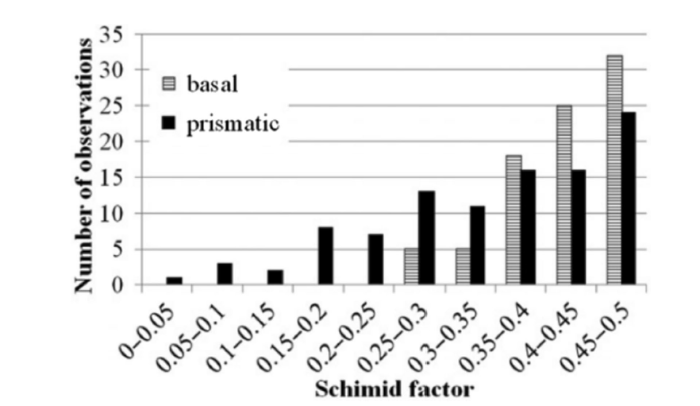
During early deformation, the slip initiation in α phase is mainly attributed to applied stress rather than internal stress. The slip system with high SF is initiated more easily due to the high SF always resulting in a large RSS [43,77]. Li et al. [78] found that the basal and prismatic slip systems with high SF could be preferentially initiated during early deformation of Ti-5Al-2.5Sn alloy. Meanwhile, as shown in Fig. 4 [78], the initiated prismatic slip systems have the wide SF distribution, whereas the initiated basal slip systems concentrate in the high SF region. It could be attributed to that the prismatic slip system is initiated more easily than basal slip system.

With the increase in strain, the slip systems with low SF that could also be initiated due to the combined effect of applied stress and internal stress [59,79]. Li et al. [80] found that some of low-SF slip systems in Ti-5Al-2.5Sn alloy could be initiated at a large strain. The initiation of low-SF slip systems (SF < 1.5) was mainly located near the grain boundaries or triple points which possess a strong local stress concentration. Bantounas et al. [81] also reported that the deformation between adjacent α grains could cause load redistribution which would affect the slip initiation behavior. In addition, Huang et al. [46] found that some α grains in Ti-6Al alloy would rotate to coordinate the larger plastic strain during deformation, which could promote the softening of hard grains and thus stimulate the initiation of low-SF slip systems.

The elastic anisotropy of α phase could significantly influence its slip initiation behavior. For the adjacent α grains in which the low-CRSS slip systems (basal and prismatic) have high SF, the slip system would be initiated more easily in α grain with higher elastic modulus during early deformation. This is because the α grain with low elastic modulus would preferentially experience elastic strain. To maintain strain compatibility, the interaction stress between the adjacent α grains is generated to raise the actual stress of high-elastic modulus α grain and then promote the slip initiation. Hémery et al. [82,83] proposed that although the SF of prismatic slip system in the grain (θ = 90°) is as higher as the SF of basal slip system in the grain (θ = 45°) in Ti-6Al-4V alloy, the grain with high elastic modulus (θ = 45°) experienced larger actual stress so that its basal slip system could be initiated more easily.

For a [0001] microtexture where the applied stress loads along the < 0001 > direction, although the elastic modulus of most α grains (θ = 0°) is the largest, the generated interaction stress is not sufficient to cause the significant slip initiation [84]. It is because that the SF of most basal and prismatic slip systems is too low to be initiated, and the high CRSS hinders the initiation of pyramidal slip system even with a high SF and at a high interaction stress. It is worth noted that a few α grains in the [0001] microtexture still possess high SF for basal and prismatic slip systems, and these grain would experience a more preferential slip initiation than other area out of the [0001] microtexture. By combining experiment with simulation, Hémery et al. [83] verified that this phenomenon was related to the relatively high actual stress experienced by the [0001] microtexture.

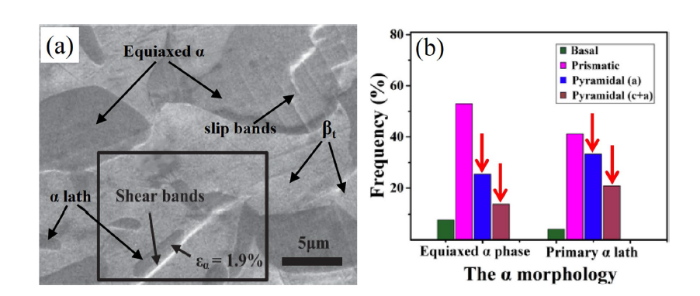
For titanium alloys, the thermomechanical processing could fabricate various microstructures with different deformation mechanisms. Some previous works revealed an effect of α grain size and morphology on slip initiation in α phase. Li et al. [69] investigated the deformation mechanism of a duplex microstructure consisting of equiaxed α grain and α colony in Ti-6Al-4V alloy and found that much fewer slip systems were initiated in lamellar α phase compared to equiaxed α grain. This is because that the small thickness of lamellar α phase restrains the nucleation and proliferation of dislocation [69,85]. In the complex microstructure consisting of fine α lath, coarse equiaxed α grain, and β_t structure (Fig. 5a [45]), Tan et al. [45] reported that the pyramidal slip system tended to be initiated in α lath rather than equiaxed α grain (Fig. 5b). For α lath, as shown in Fig. 5a, it is easier to form shear band than equiaxed α grain during deformation, and then, the resulting high stress concentration would promote the initiation of pyramidal slip in α lath.

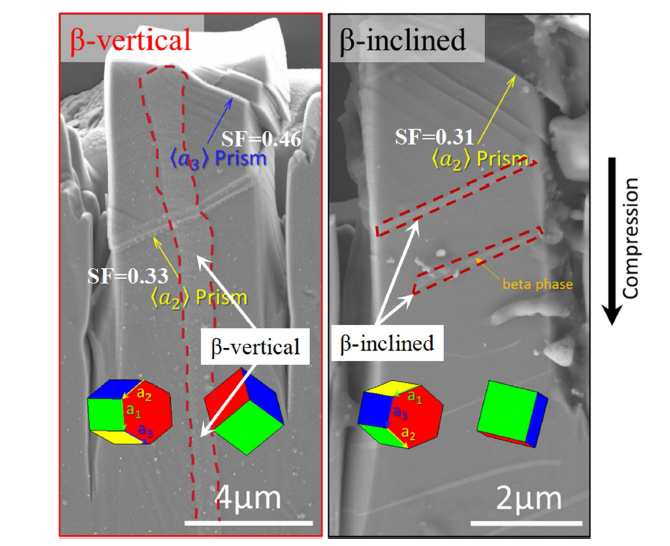
Meanwhile, Jun et al. [86] carried out an in situ micropillar compression experiment on dual-phase Ti-6242 alloy and found that the geometric distribution of interlayer β phase could significantly affect the slip initiation of lamellar α phase in α colony. As shown in Fig. 6 [86], in the β-vertical micropillar, the < a₃ > prismatic slip ($(\overline{1}100)[\overline{1}\overline{1}20]$) with the highest SF is mainly initiated. However, in the β-inclined micropillar, the < a₁ > prismatic slip ($(01\overline{1}0)[\overline{2}110]$) with the highest SF is not initiated, but the < a₂ > prismatic slip ($(10\overline{1}0)[\overline{1}2\overline{1}0]$) with the second highest is mainly initiated. This discrepancy is attributed to that the geometric distribution of β phase affects the actual stress state of α phase [52,86].

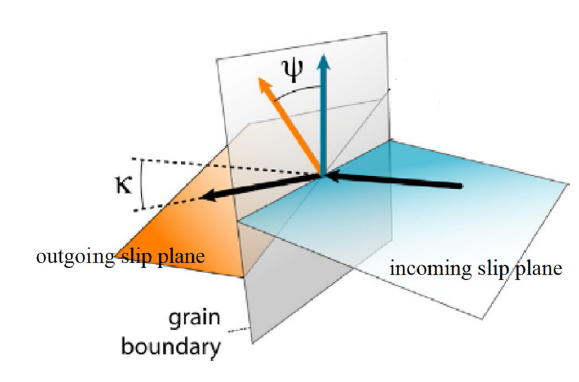
The slip transfer between adjacent grains is associated with the geometrical compatibility of the incoming and outgoing slip systems, as shown in Fig. 7 [87]. Luster et al. [88] proposed that the geometric compatibility factor ($m^{\prime }$) could be used as a parameter to predict the possibility of slip transfer, which was expressed by $m^{\prime } = \cos \kappa \cos \psi$, where $\kappa$ is the angle between slip directions, and $\psi$ is the angle between slip plane normals (Fig. 7). The $m^{\prime }$ would vary between 0 and 1. The higher $m^{\prime }$ indicates the better geometric compatibility and easier slip transfer [89,90,91,92,93]. Moreover, Lee et al. [94] argued that, in addition to the geometric relationship between slip systems, the RSS and residual dislocation at the interface should be considered for slip transfer criterion. Therefore, slip transfer between adjacent grains needs to satisfy the following three conditions: (1) good geometric relationship between the incoming and outgoing slip planes; (2) the RSS caused by the incoming slip system to the outgoing slip system is large enough; and (3) the difference of Burger vectors between the incoming and outgoing slip systems should be minimal. Meeting the three conditions implies the high probability of slip transfer.

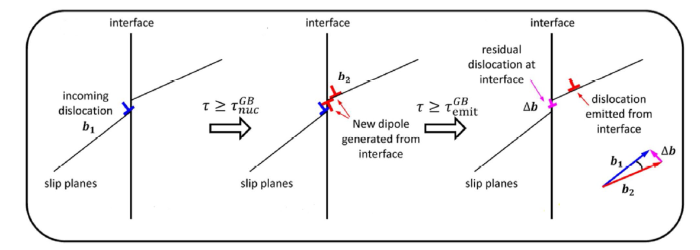
Meanwhile, it has been reported that slip transfer through an interface could be divided into indirect and direct slip transfer. For indirect slip transfer, it is associated with the nucleation of the Frank-Read sources located in front of pile-up dislocations [95,96,97]. For direct slip transfer, pile-up dislocations could be directly transferred to a new slip plane of adjacent grain [95,98,99]. Direct transfer involves dislocation re-nucleation and dislocation emission. As shown in Fig. 8 [95], the motion of the incoming dislocation (b₁) was hindered at grain or phase boundaries, resulting in dislocation pile-up and stress concentration. It would induce the formation of a new dislocation (b₂) at the interface. Subsequently, driven by the applied stress, b₂ could emit from the interface and slip along the new slip plane. But, due to the intrinsic difference between the b₁ and b₂, a small residual dislocation (Δb) is eventually generated at the interface.

The slip transfer between adjacent α grains is mainly related to the geometrical compatibility ($m^{\prime }$ value) between the incoming and outgoing slip systems. Guo et al. [100] investigated the slip transfer in pure titanium and found that the low $m^{\prime }$ value restrained the slip transfer and caused strong stress concentration at the grain boundary. In general, for adjacent soft/soft α grains with similar crystallographic orientation, the $m^{\prime }$ value is high ($m^{\prime } > 0.7$), and it is easy for slip transfer to occur [101,102,103]. Whereas, for adjacent soft/hard α grains, the $m^{\prime }$ value is low. Slip transfer from soft to hard α grains could only rely on the stress concentration caused by dislocation pile-up to activate dislocation sources in hard grain [101].

However, in addition to the $m^{\prime }$ value, slip transfer between adjacent grains is also related to the SF of outgoing slip system [100]. Yan et al. [35] reported that when the SF of outgoing slip system was low, even at a large $m^{\prime }$ value, slip transfer was impeded between adjacent α grains. Apparently, slip transfer would easily occur between adjacent α grains if both the $m^{\prime }$value and SF of outgoing slip system were relatively large [35].

As is known, α phase precipitates from the β phase with a nearly perfect Burgers orientation relationship (BOR: {0001}_α//{110}_β, < ${1}{\text{1}}\stackrel{\mathrm{-}}{2}{\text{0}}$>_α// < 111 > _β). However, this orientation relationship would be broken during deformation [104,105]. BOR and non-BOR have a significant effect on slip transfer between α and β phases.

Due to BOR, the basal plane and prismatic plane of α phase are parallel to the {110} and {112} planes of β phase, respectively, while the slip directions on two slip planes are parallel (< ${11}\stackrel{\mathrm{-}}{2}{\text{0}}$>_α// < 111 > _β), which implies the $m^{\prime }$ value of the corresponding slip systems is about 1. For example, in α colonies where α and β satisfy the BOR, basal and prismatic slip systems in α phase could easily transfer into β phase [55,106]. By using atomic force microscopy (AFM), Ambard et al. [107] found that the slip transfer between α and β phases with BOR resulted in a continuous slip band and possessed a similar height of slip steps in the two phases (Fig. 9). Tan et al. [108] found that the morphologies of the continuous slip bands varied with the different incoming slip systems in α phase. When basal slip ($(0001)[11\overline{2}0]$) transfer occurred, the slip bands in α and β were continuous without deflection (Fig. 10a) [108]. However, when prismatic slip ($(10\overline{1}0)[1\overline{2}10]$) transfer occurred, the slip bands deflected with approximately 10° at the α/β interface (Fig. 10b) [108].

For the α and β phases with non-BOR, its geometrical compatibility is relatively poor compared to BOR. However, Seal et al. [29] found that, when the outgoing slip plane with high SF in β phase was almost aligned with the incoming slip plane in α phase, slip transfer could easily occur between the two phases with non-BOR. He et al. [109] observed the same phenomenon in the absence of BOR. In addition, they also found that, when the SF of aligned outgoing slip plane in the intergranular β phase is low, slip transfer could occur between the two phases with non-BOR if the SF of other misaligned outgoing slip planes was high enough, as shown in Fig. 11 [109].

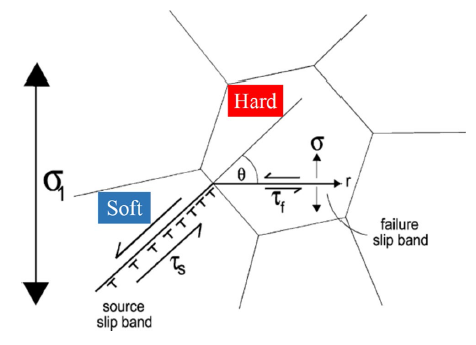
During plastic deformation, if slip could not transfer across the grain boundary or phase boundary, the dislocation pile-up on the boundary could generate a stress concentration to induce the crack nucleation [35,44,110,111]. As shown in Fig. 12 [46], during monotonic tensile deformation, the in situ observation on slip traces evolution indicated that slip was initiated in grains 1 and 2 but without slip transfer between adjacent grains. Subsequently, the stress concentration induced crack nucleation at the grain boundary (Fig. 12c). However, during cycle fatigue loading, crack nucleation in hard grain is not only associated with stress concentration caused by impeded slip bands, but also depends on the applied stress [112,113,114,115]. As shown in Fig. 13 [116,117], Stroh model [117] suggested that the impeded slip transfer could cause the stress concentration to generate a large RSS for adjacent hard grain and promote the formation of a slip band in hard grain. (This slip band is perpendicular to the direction of applied stress.) Subsequently, under the combined effect of applied stress ($\sigma_{1}$) and RSS ($\sigma$), the slip band in hard grain gradually tears to induce crack nucleation.

Additionally, in shear and slip bands, the large localized strain would make these bands lose the ability to coordinate plastic deformation and then induce crack nucleation during further deformation [44,118]. Tan et al. [45] found that, for α lath with small size, the ability to coordinate deformation was relatively poor during monotonic tensile deformation, and the formed shear band could not effectively coordinate plastic deformation to induce crack nucleation. While for equiaxed α phase with large size, the ability to coordinate deformation is better during early monotonic tensile deformation due to the formation of multiple slip bands. However, with the increase in strain, the localization of more strain within a slip band makes it impossible to further coordinate plastic deformation and finally induce crack nucleation [85,119].

The grain morphology plays an important role on crack nucleation [35,120,121], which is attributed to slip behavior. Zhou et al. [32] found that the fully lamellar and equiaxed microstructures exhibit distinct crack nucleation behavior during monotonic tensile deformation. The fully lamellar microstructure is more susceptible to crack nucleation because the relatively large colony size could produce larger effective slip length and induce more piled-up dislocations around the colony-colony interface, and then, the strong stress concentration induced the crack nucleation at the interface. However, the fully equiaxed microstructure presents very good crack nucleation resistance because the small equiaxed grains could not contain large amount of piled-up dislocations to avoid a strong stress concentration on the boundaries. Meanwhile, the residual intergranular β phase could benefit the slip transfer from α to β so as to arouse a good deformation coordination, and then relieve the stress concentration on α/β phase boundaries to restrain the crack nucleation.

Meanwhile, it has been shown that the fully lamellar microstructure is easier to form crack at the interface [32,35], while the fully equiaxed microstructure is easier to form crack in slip band [32]. It could be attributed to that the fully lamellar microstructure with a larger effective slip length could easily induce more piled-up dislocations and strong stress concentration at the interface and then induce crack nucleation [32]. However, the fully equiaxed microstructure could easily form multiple slip bands during monotonic tensile deformation, which would result in large localized strain in slip band to induce crack nucleation [32,45].

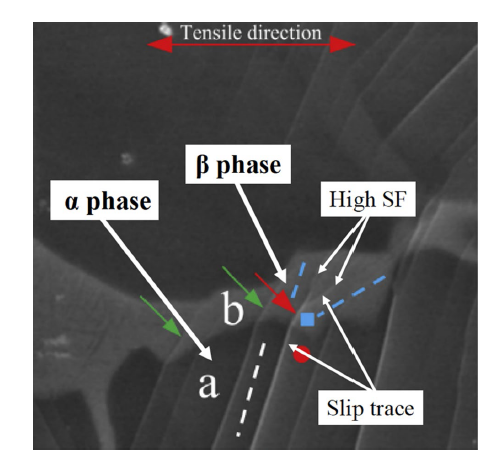
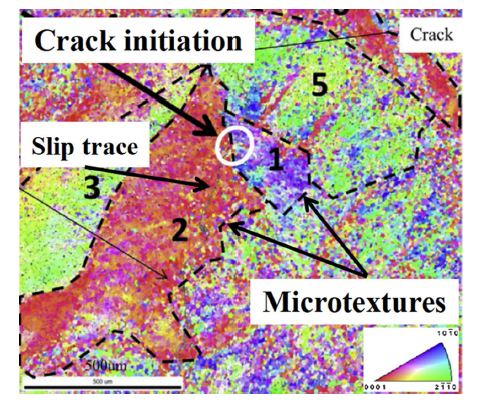
In addition, microtexture also has a significant effect on crack nucleation [122,123]. Zhang et al. [124] investigated fatigue crack nucleation in Ti-6Al-4V alloy during cycle fatigue loading and found that the interface consisting of two soft microtextures would promote crack nucleation (Fig. 14). This is because slip could easily transfer across the whole area of soft microtextures and arouse a remarkable dislocation pile-up on the microtexture-microtexture boundary to generate a large stress concentration.

In this review article, the slip initiation, slip transfer and crack nucleation mechanism in dual-phase microstructure of titanium alloys during deformation are analyzed and discussed in detail.

(1) Generally, slip is preferentially initiated in α phase during deformation because of its higher elastic modules and lower strength than β phase, and the high SF and low CRSS benefit the slip initiation in α phase. Noticeably, the alloy element would change the CRSS, and the elastic anisotropy, grain morphology, and deformation strain would influence the actual stress and SF, which subsequently affect the slip initiation in α phase.

(2) Slip transfer is mainly related to geometrical compatibility between incoming and outgoing slip systems. For adjacent α/α grains, slip transfer would easily occur if both the $m^{\prime }$ value (between incoming and outgoing slip systems) and SF of outgoing slip system are high enough. For adjacent α/β grains with BOR, the $m^{\prime }$ value is high, and slip transfer would easily occur between the two phases. For adjacent α/β grains without BOR, slip transfer could occur when the outgoing slip plane with high SF in β phase is almost aligned with the incoming slip plane in α phase.

(3) During plastic deformation, the impeded slip bands usually generate large stress concentrations at the interface to induce crack nucleation. Meanwhile, in shear and slip bands, the large localized strain would make these bands lose the ability to further coordinate plastic deformation and then induce crack nucleation. Moreover, the grain morphology and microtexture have an important influence on crack nucleation due to the difference of slip behavior.

Although scholars have carried out extensive researches on the deformation mechanism of titanium alloys, there are still the following inadequacies:

(1) More in situ experiments (SEM, TEM, synchrotron radiation) should be carried out to investigate the deformation mechanism. Meanwhile, combining experiment with simulation calculations is needed to reveal the quantitative relationship among the deformation mechanism, actual stress distribution, strain distribution, and crack nucleation.

(2) The effect of microstructure parameters on deformation mechanism needs further investigations. In particular, compared with the traditionally processing, the additive manufacture of titanium alloys fabricates a very different microstructure, but the corresponding deformation mechanism just gets a limited attention.

(3) More studies should focus on the effect of external loading condition on deformation mechanism, as well as the relationship among microstructure, deformation mechanism and mechanical properties. These results could provide a good guidance for optimizing different service performances, including tensile properties, fracture toughness, creep resistance, impact toughness, and so on.

This work is supported by the National Natural Science Foundation of China (Grant No. 51971046).

Conflict of interest The authors state that there are no conflicts of interest to disclose.