The hot deformation and dynamic recrystallization (DRX) behavior of austenite-based Fe-27Mn-11.5Al-0.95C steel with a density of 6.55 g cm-3 were investigated by compressive deformation at the temperature range of 900-1150 °C and strain rate of 0.01-10 s-1. Typical DRX behavior was observed under chosen deformation conditions and yield-point-elongation-like effect caused by DRX of δ-ferrite. The flow stress characteristics were determined by DRX of the δ-ferrite at early stage and the austenite at later stage, respectively. On the basis of hyperbolic sine function and linear fitting, the calculated thermal activation energy for the experimental steel was 294.204 kJ mol-1. The occurrence of DRX for both the austenite and the δ-ferrite was estimated and plotted by related Zener-Hollomon equations. A DRX kinetic model of the steel was established by flow stress and peak strain without considering dynamic recovery and δ-ferrite DRX. The effects of deformation temperature and strain rate on DRX volume fraction were discussed in detail. Increasing deformation temperature or strain rate contributes to DRX of both the austenite and the δ-ferrite, whereas a lower strain rate leads to the austenite grains growth and the δ-ferrite evolution, from banded to island-like structure.
Fe-Mn-Al-C steel has been highly recognized as a promising auto-body material because of the excellent mechanical properties, low density, and corrosion resistance, which could be developed to reduce energy consumption and CO2 emission [1]. Such excellent mechanical properties rely on the addition of light element such as C, Al, and Mn, which also determine the phase structure[2]. Based on the proportion of austenitic stable elements (Mn, C) and ferrite forming elements (Al, Si), Fe-Mn-Al-C steel could be distinguished into single austenite (γ ) [3], austenite-based (γ + little δ + κ ) [4], and ferrite-based structures (α + retained γ + κ ) [5]. Many reports have focused on the deformation mechanism and continuous strain hardening behavior of Fe-Mn-Al-C steel at room temperature and proved that the austenite-based duplex steel has higher tensile strength and weight reduction [6]. The optimal comprehensive performance depends on the chemical composition and reasonable processing technology. However, the hot deformation and DRX of high alloyed austenite/δ -ferrite Fe-Mn-Al-C steel, which may be a useful reference for processing parameter design, have not been studied systematically.
The coexistence of austenite and second-phase δ -ferrite makes hot deformation complex, but is similar to the characteristic of Cr-Ni duplex stainless steel (DSS). Balancin et al.[7] and Duprez et al. [8] found that the δ -ferrite phase in DSS exhibits a continuous DRV during hot deformation because of its high stack fault energy, while the austenite phase undergoes DRX with a limited DRV. It agrees with the observed numerous low-angle boundaries inside the large δ -ferrite grains of duplex 25Mn8Al deformed to a strain of 0.8 by Hamada et al. [9]. DRX is also influenced by the volume fraction of each phase and the deformation parameters, such as temperature, strain rate, and deformation degree [10]. Fan et al. [11] made completely inverse conclusions when studying DRX behavior of 2205 DSS deformed within a range of 750-1350 ° C, and they found that only DRV occurred within the austenite phase, but the δ -ferrite phase was characterized by DRX.
DRX is a fundamental characteristic for microstructure control in the grain size and mechanical properties during hot deformation, which makes the study essential. In our work, an austenite-based Fe-27Mn-11.5Al-0.95C steel with a weight reduction of 16.6% was developed to examine flow curve characteristics, DRX kinetics, and the relationship between DRX microstructure and deformation conditions by systematic hot compression tests. The steel containing a small amount of δ -ferrite underwent extensive plastic deformation under wide temperature range and strain rates. The yield-point-elongation-like effect caused by δ -ferrite DRX was quantified by Zener-Hollomon parameter for the first time, as well as austenite DRX. The effects of deformation parameters on DRX kinetics and microstructure evolution were described in detail. The findings could serve as a reference for further research on austenite-based low-density Fe-Mn-Al-C steel.
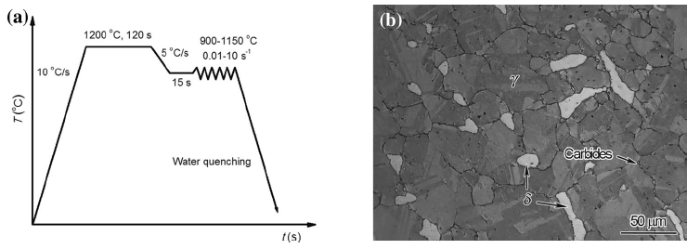
A 20 kg ingot of Fe-Mn-Al-C steel was prepared in vacuum induction melting furnaces with measured compositions (wt%) of 0.95C, 0.59Si, 27.02Mn, 11.5Al, 0.043Nb, and Fe in balance. Homogenized at 1150 ° C for 2 h, the as-cast ingot was forged into billet with a section dimension of 40 mm × 80 mm. Cylindrical specimens with 15 mm in height and 8 mm in diameter were machined directly from the forged billet. Gleeble-1500 thermal-mechanical simulator was employed to perform hot compression test at the temperature range of 900-1150 ° C at an interval of 50 ° C and strain rate of 0.01-10 s-1. As shown in Fig. 1a, the specimens were heated at a rate of 10 ° C/s to 1200 ° C, soaked for 120 s in order to eliminate the segregation of the alloying elements, and cooled to the test temperature with a cooling rate of 5 ° C/s. All specimens were compressed to a true strain of 0.9, and water quenched immediately to room temperature within about 5 s. The microstructures of sectioned at mid-plane perpendicularly to the compression direction were optically examined. The initial microstructure of the forged steel is shown in Fig. 1b consisting of the austenite and ~6% δ -ferrite phases. Meanwhile, the observed fine carbides at the grain boundaries would be dissolved in the matrix completely as heated to 1200 ° C. JEM 2100 transmission electron microscope (TEM) was used to observe the microstructure of the sample deformed to a certain strain at 900 ° C and strain rate of 0.1 s-1. Twin-jet polishing technique (5% perchlorate alcohol at -30 ° C, applied potential of 50 V) was implemented to prepare thin foil samples for TEM observation. The measured density of the steel by a Sartorius BSA 2245 electronic analytical balance was 6.55 g cm-3, with an apparent reduction of 16.6% in comparison with pure iron.
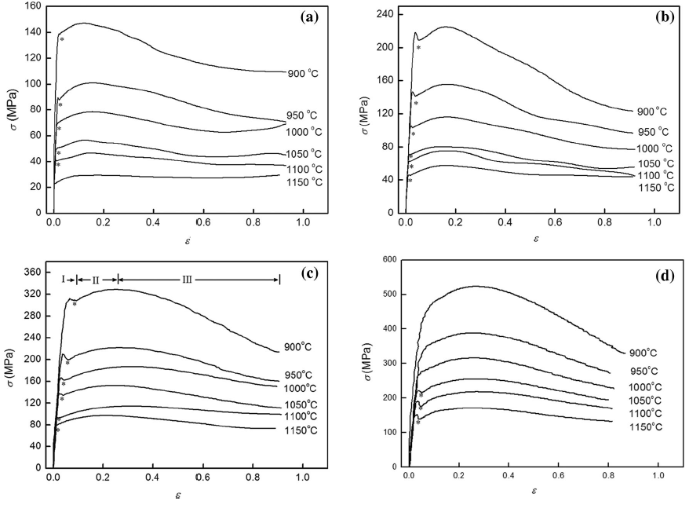
Figure 2 shows the flow stress-strain curves of the steel deformed at various temperatures and strain rates. Most curves could be divided into three sections in accordance with the developing trend of flow stress, such as the curve at 900 ° C and 1 s-1. In the first section, i.e., the early stage of deformation, a flow rapid increase caused by strong work hardening effect was followed by a remarkable drop with increasing strain in some curves, called yield-point-elongation-like effect[8].
Pronounced upper and lower yielding points could be observed. These phenomena were observed during hot deformation of DSS and explained by the heterogeneous strain between the austenite/δ -ferrite phases [12, 13, 14]. However, this phenomenon did not occur for the specimens at a high temperature with a low strain rate or at a low temperature with a high strain rate, such as the curve deformed at 900 ° C and 10 s-1. At the second section, the work hardening effect occupied the dominant position again until DRX of the austenite occurred [15]. Flow stress increased slowly with increasing deformation strain, then reached a peak, and followed by a gradual fall at the third section, which indicated that the steel has typical DRX characteristics under the present deformation conditions. In some curves, flow stress developed toward a steady region and increased slightly afterward. From Fig. 2, it is also seen that both the peak stress (σ p) and the peak strain (ε p) for the experimental steel increased with the decrease in temperature and increase in strain rate.
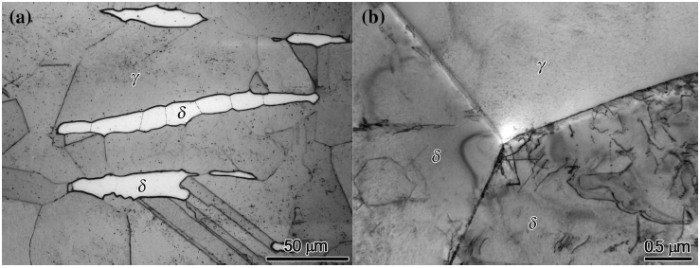
As is known that the strength of the steel at the early stage of hot deformation was determined by both strain hardening and dynamic softening, and the coexistence of the δ -ferrite and the austenite made it complex. The microstructure of the sample deformed to the yield strain (ε y, the lower point) of 0.0535 at 900 ° C and 0.1 s-1 shown in Fig. 3a indicates that the δ -ferrite was compressed to a banded structure with high angle grain boundaries inside. Curved dislocations were distributed randomly in δ -ferrite and tangled at the recrystallization grain boundaries, as shown in Fig. 3b. Hence, not only DRV but also DRX occurred in the banded δ -ferrite at the early stage of deformation. By contrast, equiaxial austenite with annealing twins inside only underwent grain growth and boundary migration at high temperature. Reported literatures showed that the austenite phase with a high stack fault energy, especially at high temperature, exhibited typical planar dislocation slip characteristics [16, 17]. But no dislocation enrichment was found in the austenite at this stage. Given the difference in hot strength, the harder austenitic phase offers more resistance to plastic deformation than softer δ -ferrite [18]. Strain was mainly accommodated to softer δ -ferrite, resulting in a higher dislocation density than austenite. Except for the inhomogeneous strain partitioning between the austenite and δ -ferrite, the concentration of ferrite former elements, especially the Al, also made the δ -ferrite higher stack fault energy and easier to proceed cross-slip and DRX. Once the ε y for δ -ferrite DRX was reached, the strain energy accumulated during hot deformation would be released suddenly with a drop of flow stress. The inhomogeneous strain partitioning and δ -ferrite DRX lead to the recorded yield-point-elongation-like effect at the early stage. With increasing strain, load was transferred from δ -ferrite to austenite, which lead to an increase in dislocation density and flow stress until DRX of austenite occurred. Different from traditional yield effect of the steel at room temperature explained by Cottrell-Billy theory or phase transformation[13], this kind of yield point effect occurs in the duplex steel at high temperature with dynamic softening.
The constitutive characteristics of the experimental steel were studied to investigate the DRX behavior and the effects of deformation temperature and strain rate on the flow stress by Zener-Hollomon parameter [Eq. (1)], which reflects how difficult DRX occurs [18]. Hyperbolic sine function [Eq. (2)] has been proved to give the highest approximation in three known types of stress functions by regression calculation and could be used to analyze the DRX behavior under any condition[19, 20].
$$Z = \dot{\varepsilon }\exp \left( {\frac{Q}{RT}} \right). (1)$$
$$\dot{\varepsilon } = A\left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right]^{n} \exp \left( { - \frac{Q}{RT}} \right). (2)$$
where \(\dot{\varepsilon }\) is the strain rate (s-1); Q is the thermal activation energy for hot deformation (J mol-1); R is the universal gas constant (8.3145 J mol-1 K-1); T is the absolute temperature (K); A, a, and n are the material constants; σ p is the peak stress obtained from the true stress-strain curves. After taking logarithm for both sides of Eq. (2), it can be written as follows:
$$\ln \dot{\varepsilon } = \ln A + n\ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right] - \frac{Q}{RT}. (3)$$
On the basis of Levenberg-Marquardt and global optimization method, the data were processed repeatedly by 1stOpst15PR software, and the value of Q could be obtained as 294.204 kJ mol-1 within the temperature of 900-1150 ° C. The values for α , n, and A were 0.003470, 3.9284, and 3.167 × 1012, respectively. For constant T, Eq. (3) could be rewritten as Eq. (4) after taking the derivative, and Eq. (5) could be obtained for constant \(\dot{\varepsilon }\) [21].
$$n = \left[ {\frac{{\partial \ln \dot{\varepsilon }}}{{\partial \ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right]}}} \right]_{T} . (4)$$
$$Q = \left[ {Rn\frac{{\partial \ln \left[ {\sinh \left( {\alpha \sigma_{\text{p}} } \right)} \right]}}{{\partial \left( {1/T} \right)}}} \right]_{{\dot{\varepsilon }}} . (5)$$
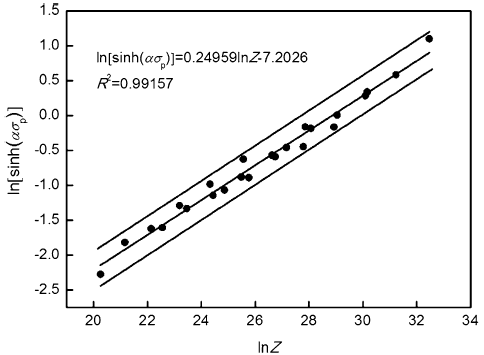
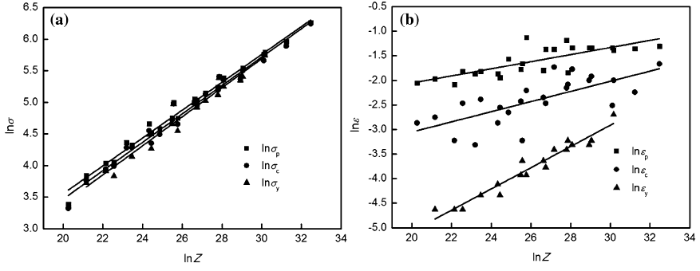
In accordance with the relationship curves of \(\ln \dot{\varepsilon } - \ln [\sinh (\alpha \sigma_{\text{p}} )]\) (Fig. 4a) and \(\ln [\sinh (\alpha \sigma_{\text{p}} )] - 1/T\) (Fig. 4b), hyperbolic sine law is suitable for the austenite-based Fe-Mn-Al-C steel with a high coefficient of determination. From Eqs. (1) and (2), the plots of \(\ln [\sinh (\alpha \sigma_{\text{p}} )]\) versus ln Z may present the linear relationship between σ p and Z. The corresponding curve is shown in Fig. 5, and the hyperbolic sine function with the calculated values is developed as follows:
$$Z = \dot{\varepsilon }\exp \left( {\frac{294204}{RT}} \right) = 3.167 \times 10^{12} \left[ {\sinh \left( {0.00347\sigma_{\text{p}} } \right)} \right]^{3.9284} . (6)$$
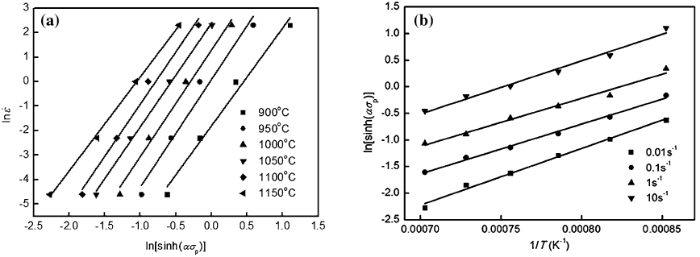 | Fig. 4 Relationship between a \(\ln \dot{\varepsilon }\) and \(\ln [\sinh (\alpha \sigma_{\text{p}} )]\), b \(\ln [\sinh (\alpha \sigma_{\text{p}} )]\) and 1/T |
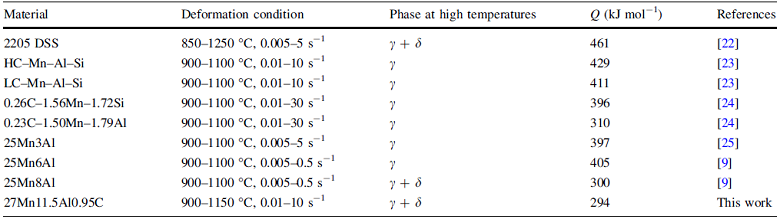
The activation energy is an important parameter to indicate the difficulty of hot deformation and is influenced mainly by the alloy element content. Table 1 shows the activation energy of some steels by hot compression. The calculated value of the activation energy was far below than that of duplex stainless steel, 460 kJ mol-1 for 2205 DSS [22], for example. The effects of Mn, Al, and C elements on activation energy were not high as solute content of Cr, Mo, and Ni additions in stainless steels. Khosravifard [23] reported that the values of the activation energy were 429 kJ mol-1 for high C and 411 kJ mol-1 for low C steels, respectively. However, with such a high C content of 0.95% for the steel, the activation energy was lower that other high Mn steel. Wei et al. [24] compared 0.26C-1.56Mn-1.72Si (wt%) based and 0.23C-1.50Mn-1.79Al (wt%) based microalloyed high-strength steels, and found that the activation energy approximately 310 kJ/mol for high Al steel was lower than that (396 kJ mol-1) for high Si steel. Hamada et al. [9, 25] investigated the effect of Al addition from 3% to 8% in Fe-25Mn steel on the activation energy during hot deformation. With the single austenite structure, the activation energy of 25Mn6Al (405 kJ mol-1) was higher than that (397 kJ mol-1) of 25Mn3Al steel, indicating that Al addition helps to increase the activation energy, whereas the calculated activation energy for the experimental steel was somewhat close to the 300 kJ mol-1 for 25Mn8Al steel because of the same characteristic of austenite/δ -ferrite duplex structure at high temperatures. The dynamic softening effect, especially the DRX of δ -ferrite, would absorb parts of deformation energy and reduce peak stress of flow curves. It can be seen that with the same strain rate, the softening effect of δ -ferrite DRX at low temperature was larger than that at high temperature (Fig. 2b), which would decrease the sensitivity of \(\ln [\sinh (\alpha \sigma_{\text{p}} )]\) to 1/T. It responds as lower calculated activation energy than that of single austenite Fe-Mn-Al-C steel.
| Table 1 Data for the activation energy for some steels obtained by compression |
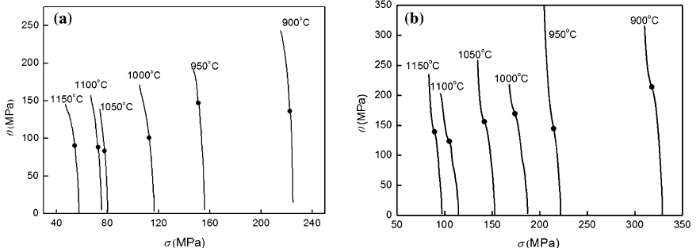
DRX would occur as the deformation strain reaches a certain level. The first step for studying DRX is to learn the critical recrystallization strains (ε c) and the critical stresses (σ c). The strain for δ -ferrite DRX, at which the flow stress reaches the bottom, could be counted from the flow stress curves, so as ε c for austenite DRX by calculating the inflection point of \(\theta ({\text{d}}\sigma /{\text{d}}\varepsilon ) - \sigma\) curves [26, 27]. The strain hardening rate values were calculated as a function of flow stress, and the θ -σ curves at various temperatures and strain rates of 0.1 and 1 s-1 are shown in Fig. 6.
It indicates that the σ c for austenite DRX decreases with increasing deformation temperature. The relationships of all the flow stress and strains of characteristic points with Z parameter are shown in Fig. 7. In accordance with the liner relationship by regression analysis, the following equations could be obtained:
$$\sigma_{\text{p}} = 0.423 Z^{ 0.221} .(7)$$ $$\sigma_{\text{c}} = 0.357 Z ^{0.225} .(8)$$ $$\sigma_{\text{y}} = 0.300 Z ^{0.230} . (9)$$$$\varepsilon_{\text{p}} = 3.02 \times 10^{ - 2} Z ^{0.00726} . (10)$$
$$\varepsilon_{\text{c}} = 5.98 \times 10^{ - 3 } Z^{ 0.103} .(11)$$ $$\varepsilon_{\text{y}} = 8.27 \times 10^{ - 5} Z ^{0.216} . (12) $$
Despite the poor dependence of ε c and ε p on Z parameter (Fig. 7b), both the flow stress and corresponding strain for DRX of the δ -ferrite and the austenite would increase with increasing Z parameter. It can be seen that this kind of typical yield point phenomena shows the same dependence on temperature and strain rate, in accordance with the results by Abbasi et al. [28]. Increasing temperature or decreasing strain rate contributed to DRX for both δ -ferrite and austenite. For example, at a strain rate of 0.1 s-1, the true strains for the yield-point-elongation-like effect at 900-1000 ° C were 0.0500, 0.0346 and 0.0264, respectively, decreasing with increasing deformation temperature. This result was due to the fact that the deformation strain stored for DRX of δ -ferrite at a low temperature is larger than that at a high temperature, and increasing deformation temperature or decreasing strain rate helps to enhance this type of dynamic softening effect.
Although the yield-point-elongation-like effect was not observed at too high or low Z parameters from the flow stress curves, DRX of δ -ferrite did occur. The dynamic softening effect was covered completely by work hardening as deformed at low temperature and high strain rate, whereas the strain energy at high temperature and low strain rate was released gradually by DRV, because more time was needed to reach the ε y. Hence, the yield-point-elongation-like effect, that is, drop flow stress, was not as obvious as the other deformation situations.
The flow stress curves in Fig. 2 indicate that DRX was the main dynamic softening effect during hot deformation for the austenite-based steel, and DRX of the austenite dominated at the later stage. Determining the DRX fraction by microstructure observation is generally difficult, but it can be derived from the flow curves and expressed as follows [29]:
$$X = \frac{{\sigma_{\text{p}} - \sigma }}{{\sigma_{\text{p}} - \sigma_{\text{s}} }}. (13)$$
where σ p is the peak stress and σ s is the steady state stress. The (σ p-σ s) term indicates the maximum softening without considering the DRV and DRX of the δ -ferrite, and the (σ p-σ ) term indicates the DRX softening degree with increasing strain. Equation (14) can be used to simplify the Avrami-type model with acceptable accuracy.
$$X = 1 - \exp \left( { - k\left( {\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }}} \right)^{n} } \right). (14)$$
where k and n are the material constants; ε is the true strain. Although ε c is known as the critical strain for the initiation of DRX, flow softening actually starts at ε p[27]. Meanwhile, the preceding analysis showed poor dependence of ε c on Z parameter. In order to reduce the error factors, Eq. (14) can be expressed as follows [30]:
$$X = 1 - \exp \left( { - k\left( {\frac{{\varepsilon - \varepsilon_{\text{p}} }}{{\varepsilon_{\text{p}} }}} \right)^{n} } \right). (15)$$
Figure 8 shows the almost linear relationship between \(\ln \ln \left( {1/\left( {1{-}X} \right)} \right)\) and \(\ln ((\varepsilon {-}\varepsilon_{\text{p}} )/\varepsilon_{\text{p}} )\) under various deformation situation with the acquired value of k and n. Hence, the kinetic model of DRX for the experimental steel can be expressed as follows:
$$X = 1 - \exp \left( { - 0.3396\left( {\frac{{\varepsilon - \varepsilon_{\text{p}} }}{{\varepsilon_{\text{p}} }}} \right)^{1.747} } \right). (16) $$
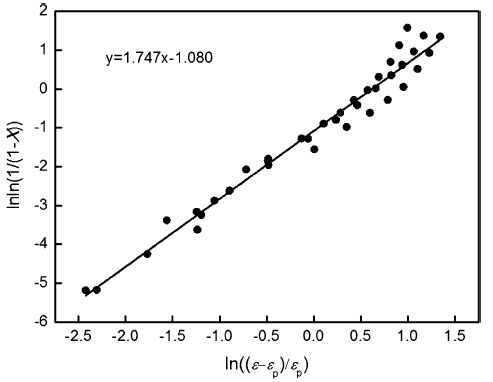 | Fig. 8 Relationship between the \(\ln \ln \left( {1/\left( {1 - X} \right)} \right)\) and \(\ln ((\varepsilon - \varepsilon_{\text{p}} )/\varepsilon_{\text{p}} )\) |
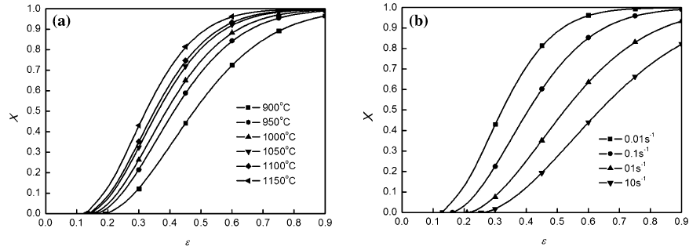
According to the calculated result of DRX model, the effects of deformation temperature and strain rate on DRX volume fraction are shown in Fig. 9, which indicated that the volume fraction of DRX increased with increasing deformation strain and that DRX is faster at a high temperature or a low strain rate. As deformed to a strain of 0.9, incomplete recrystallization occurred at a low temperature and high strain rate. The calculated DRX volume fraction at 1150 ° C and 10 s-1 was only 0.822, for example. And the effect of strain rate was larger than that of temperature with the conditions.
The analysis above indicated that the DRX was dependent sensitively on the deformation temperature and strain rate for the steel. Thus, the effects of deformation temperature and strain rate on the microstructure were investigated, as shown in Fig. 10. The central part of the hot deformation samples was chosen as the area for microstructure observation, because it represented the real deformation state. As expected, the sizes of new DRX austenite grains increase with decreasing strain rate and increasing temperature. With the same strain rate of 1 s-1, the optical microstructures (Figs. 10a-c) showed a duplex structure consisting of the recrystallization austenite and the banded δ -ferrite. In Fig. 10a, obtained at 900 ° C and strain rate of 1 s-1, the original grains were elongated, and fine DRX was nucleated at intimal austenite boundaries or γ /δ interfaces. With increasing deformation temperature, the DRX volume fraction and the grain size of the austenite increased significantly, and the original grains were replaced by DRX grains completely, as seen in Fig. 10c. Figure 10c-f shows the DRX microstructure deformed at 1100 ° C with various strain rates. Except for increasing DRX austenite grains, the morphology of δ -ferrite changed from banded structure at strain rate of 10 s-1to island-like at strain rate 0.01 s-1. That is because considerable time was needed at a low strain rate to generate the given strain, and DRV would decrease intracrystalline defect density and the austenite nucleation, thereby resulting in austenite growth and boundary migration. The grain boundary of the austenite expanded to outside gradually and separated the banded δ -ferrite into island-like structure, which was distributed in the austenite matrix discontinuously. However, at high strain rates, the growth of the austenite grains was too small to have a significant effect. Therefore, it can be concluded that the δ -ferrite morphology after hot deformation was mainly determined by the strain rate, that is, banded structure at high strain rate and island-like at low strain rate. It was acted on together by internal δ -ferrite DRX and external austenite grain growth. Increasing deformation temperature at low strain rate could also promote grain growth for both the austenite and the δ -ferrite. Coarsening austenite and δ -ferrite grains were obtained as deformed at 1100 ° C and strain rate of 0.01 s-1(Fig. 10d). Hot deformation parameters would affect the volume fraction and morphology of each phase, so further investigations are necessary for providing the evidences of DRX behavior for both the austenite and the δ -ferrite.
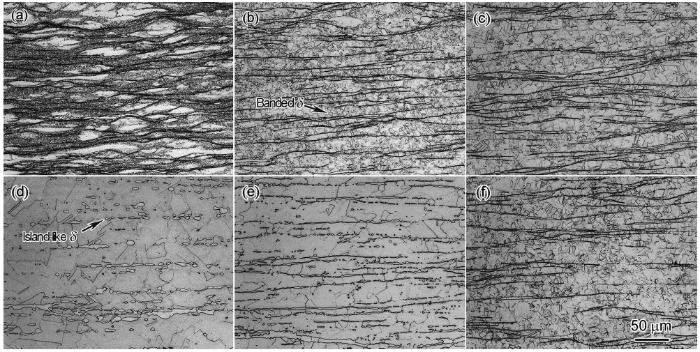 | Fig. 10 Optical microstructures of the samples deformed under various conditions: a 900 ° C, 1 s-1, b 1000 ° C, 1 s-1, c 1100 ° C, 1 s-1, d 1100 ° C, 0.01 s-1, e 1100 ° C, 0.1 s-1, f 1100 ° C, 10 s-1 (The compression direction is vertical) |
1.The flow stress curves of the experimental steel showed DRX characteristic with any chosen deformation temperatures and strain rates. The peak stress of isothermally compressed steel increased significantly with lower temperature and higher strain rate. The phenomenon of yield-point-elongation-like effect was explained by the heterogeneous strain between dual phases and δ -ferrite DRX.
2.The flow stress constitutive equation of the steel was developed by hyperbolic sine function with calculated activation energy of 294.204 kJ mol-1. The dependence of the characteristic flow stress and strain on Z was obtained as σ p = 0.423Z 0.221, σ c= 0.357Z 0.225, σ y = 0.300Z 0.230, ε p = 3.02 × 10-2 Z 0.00726, ε c = 5.98 × 10-3 Z 0.103 and ε y = 8.27 × 10-5 Z 0.216.
3.The DRX kinetic model of the austenite-based steel was established as \(X = 1 - \exp \{ - 0.3396[(\varepsilon - \varepsilon_{\text{p}}) /\varepsilon_{\text{p}} ]^{1.747} \}\) without considering DRV and δ -ferrite DRX.
4.Microstructure observation showed that DRX of experimental steel was sensitive to deformation temperature and strain rate. Increasing deformation temperature or decreasing strain rate would promote DRX and growth for both the austenite and the δ -ferrite. Austenite grain growth at low strain rate contributed to the evolution of δ -ferrite morphology, from banded to island-like structure.
The authors would like to express their gratitude to the Materials Testing Centre at the University of Science and Technology Beijing for the access to the Gleeble-1500 thermal-mechanical simulator and to Beijing General Research Institute of Mining and Metallurgy for TEM observation.
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|