3.1.1 X-ray Diffraction

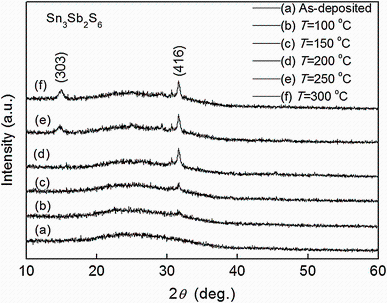
Figure 1 shows the X-ray diffraction (XRD) patterns of Sn₃Sb₂S₆ thin films prepared at the same deposition parameters and annealed at different temperatures. The identification and assignment of the phases and crystal structure from observed diffraction patterns were made by comparison of the diffraction peaks with standard diffraction peak values of 38-0826 data. Figure 1 shows that crystalline modifications depend upon annealing temperatures which is proved for many other materials [18]. The annealing temperature 150 ° C acted as a transition stage of recrystallization and showed very poor crystalline structure. This result was found by others researchers in similar compounds [15]. Diffraction patterns of the films annealed at 200 ° C showed a peak of orthorhombic Sn₃Sb₂S₆ phase with (416) reflection at 31.70° . When we increased annealing temperature to 250 ° C, additional peak appeared to be at 14.84° with (303) reflection. This peak corresponds to the Sn₃Sb₂S₆ phase. In addition, annealing temperatures affect the peaks’ intensities. In fact, they are less at lower annealing temperatures while become higher with increased temperatures. Indeed, the crystallinity of the films increases by increasing the annealing temperature. This result was found by others researchers for many compounds [19, 20]. It is also noticed that no oxides phases were detected. By comparison, the SnSb₂S₄ and Sn₂Sb₂S₅ thin films prepared in the same conditions we note the presence of the Sb₂O₄ as secondary phase [21, 22].

Fig. 1

	Figure Option ViewDownloadNew Window
	Fig. 1 XRD patterns of Sn3Sb2S6 thin films as-deposited and annealed at different temperatures

3.1.2 Microstructural Parameters

The crystallite size of Sn₃Sb₂S₆ thin films was calculated from the (416) peaks using Scherrer’ s formula [23]:

(1)

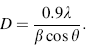
where λ is the X-ray wavelength, β is the full width at half maximum (FWHM) measured in radian and θ is the Bragg angle. In the higher annealing region (250-300 ° C) crystallites grew bigger in size with comparison with lower annealing temperature (200 ° C). This behavior is proved by many other studies [24, 25] and is a characteristic of recrystallization and reorientation of planes.

The dislocation density (δ ), defined as the length of the dislocation lines per unit volume of crystal, is evaluated using the formula [26]:

(2)

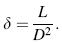
where L is a factor that equals unity when the dislocation density is minimum and D is the crystallite size.

The lattice strain ε was calculated by using the Scherrer’ s relation [23]:

(3)

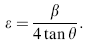
The stacking fault probability α , which is defined as the fraction of the layer that undergoes stacking sequence faults in a given crystal, is given by [27]:

(4)

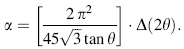
The stacking fault probabilities were calculated from the shift of the peaks of the X-ray lines of the films with reference to the 1997 JCPDS database No: 38-0826 using Eq. (4).

The microstructural parameters are given in Table 1. The crystallite size and the stacking fault probabilities increase, but the dislocation density and the strain decrease by increasing the annealing temperature. The decrease in the strain indicates the formation of higher quality film at higher temperature [28, 29]. The stacking fault probability rise is probably related to the variation in the interplanar spacing and the stresses built up in the film [30].

Table 1

Table 1

Table 1 Estimated values of the microstructural parameters of Sn3Sb2S6 thin films annealed at different temperatures T (° C) D (nm) ε δ (10-3 nm-2) α 200 20 0.38 2.50 0.01 250 23 0.36 1.80 0.20 300 24 0.31 1.70 0.25

Table 1 Estimated values of the microstructural parameters of Sn3Sb2S6 thin films annealed at different temperatures

3.2.1 Transmittance and Reflectance Spectra

Figure 2a, b shows the optical transmittance spectra T and reflectance spectra R of Sn₃Sb₂S₆ thin films at normal light incident in the wavelength range 300-1800 nm.

Fig. 2

	Figure Option ViewDownloadNew Window
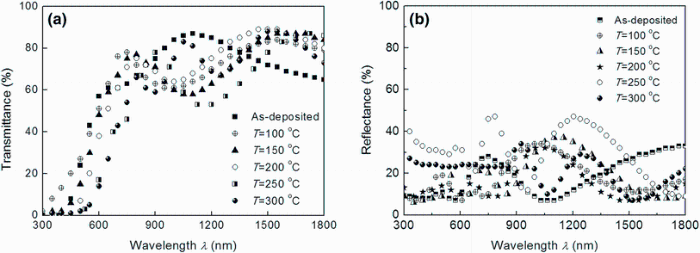	Fig. 2 Transmittance a and reflectance spectra b of Sn3Sb2S6 thin films as-deposited and annealed at different temperatures

It is seen that the interference effects disappear in the region of very strong absorption, while the maximum amplitude is observed in the transparent region. It should be also seen that for all thin films in the transparent region, almost R + T = 1, which falls within the experimental error which indicates no scattering or absorption in this region. These results proved the homogeneity of the deposited films [31].

3.2.2 Absorption Coefficient, Energy Band Gap and Extinction Coefficient

The optical absorption coefficient α of the investigated films is evaluated from the experimental data of transmittance and reflectance in strong absorption region using the relation [32]:

(5)

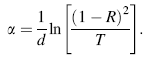
where α is the absorption coefficient and d is the film thickness, R and T are the reflection and transmission coefficients, respectively. Figure 3 shows the absorption coefficients versus the photon energy for the thin films annealed at different temperatures.

Fig. 3

	Figure Option ViewDownloadNew Window
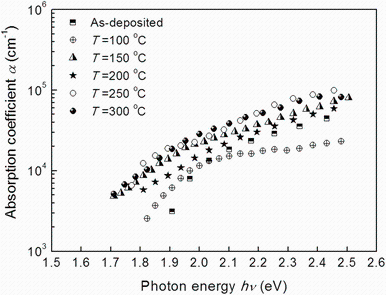	Fig. 3 Absorption coefficient spectra of Sn3Sb2S6 thin films as-deposited and annealed at different temperatures

The low wavelength absorption data for the deposited Sn₃Sb₂S₆ thin films are related to the fundamental absorption, which refers to the band-to-band transition, i.e., to the excitation of an electron from the valence band to the conduction band. It can be seen that all the films have relatively high absorption coefficients (10⁵ cm^-1) in the visible and near-IR spectral range.

The fundamental absorption can be used to determine the nature and value of the optical band gap. The absorption coefficient α can be related to the energy gap E_g by applying the model postulated by Davis and Mott [33]:

(6)

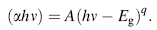
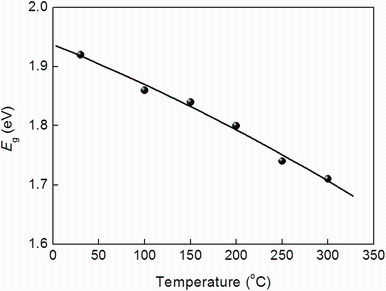
where A is a constant, h is the Planck constant, ν is the frequency of the incident beam and q is equal to ½ to a direct gap. To determine the possible transitions, we plot (α hν )² versus photon energy hν (Fig. 4). These plots indicated that, in photon energy range 1.5-2 eV, a linear plot is obtained corresponding direct optical transition [16]. The band gap values decrease with the increase in annealing temperature (in the range 1.92-1.71 eV). The effect of the annealing on the band gap values is proved for many other compounds [25]. It may be related to the improvement in crystallization of the thin films [34].

Fig. 4

	Figure Option ViewDownloadNew Window
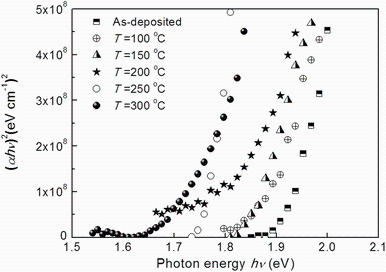	Fig. 4 Plots of (α hν )2 versus hν for Sn3Sb2S6 thin films as-deposited and annealed at different temperatures

Figure 5 shows the variation in the estimated band gap values of the films with the different temperatures. The direct band gap values decrease with the increase in the temperatures which are comparable to those reported by Arbi et al. [16]. The dependence of the direct band gap E_g on the temperature can be fitted to a second-degree polynomial function:

(7)

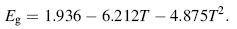
The extinction coefficients k(λ ) of Sn₃Sb₂S₆ thin films were calculated using the following expression [35]:

(8)

Fig. 5

	Figure Option ViewDownloadNew Window
	Fig. 5 Variation in Eg with the temperature of annealing for the Sn3Sb2S6 thin films

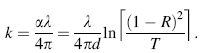
Figure 6 shows the dependence of k on the wavelength for Sn₃Sb₂S₆ thin films. The extinction coefficient decreases with the increase in the wavelength showing the decrease in the fraction of light lost due to scattering and absorbance [36]. In addition, the optical absorption edge can be seen clearly for all thin films.

Fig. 6

	Figure Option ViewDownloadNew Window
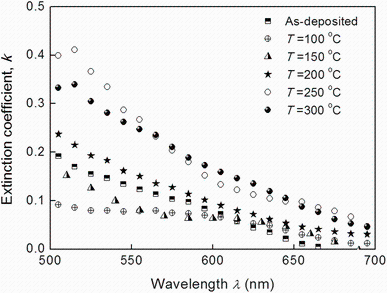	Fig. 6 Variation in the extinction coefficient, k with wavelength for Sn3Sb2S6 thin films as-deposited and annealed at different temperatures

3.2.3 Optical Refractive Index, n

Due to the existence of the interference patterns, the method of Swanepoel was used to calculate the refractive index n from the relation [37, 38]:

(9)

(10)

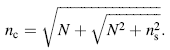
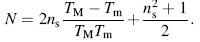
Here n_s is the refractive index of the glass substrate.

T_max and T_min are the values of the envelope at the wavelengths where the upper and lower envelops and the experimental transmittance spectrum are tangential. Figure 7 shows that for all the investigated samples, the refractive index decreases sharply at the wavelength of 700 nm, which is corresponding to the optical band gap of this material and becomes fairly flat above 1000 nm showing normal dispersion behavior. It is also noted that the magnitude of refractive index increases notably with increasing the annealing temperature. The observed refractive index values are in good agreement with the reported values of others Sn-Sb-S thin films prepared in the same conditions [21].

Fig. 7

	Figure Option ViewDownloadNew Window
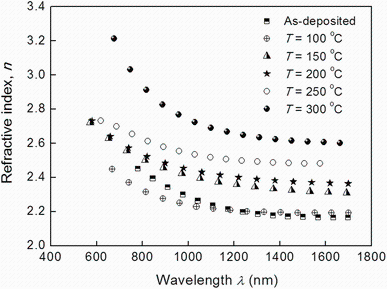	Fig. 7 Variation in the refractive index with wavelength for Sn3Sb2S6 thin films as-deposited and annealed at different temperatures

3.2.4 Refractive Index Dispersion Analysis

Refractive index dispersion data below the interband absorption edge were analyzed using a single-effective-oscillator fit proposed by Wemple [39]:

(11)

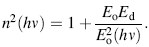
where hν is the photon energy, E_o is the oscillator energy and E_d is the dispersion energy. E_d is a measure of the average strength of the interband optical transitions, and E_o defines the average energy gap usually considered as the energy separation between the centers of both the conduction and the valence bands. The values of E_d and E_o are obtained from the intercept and the slope resulting from the extrapolation of the curve of Fig. 8. This curve represents plots of (n² - 1) ^-1 versus (hν )² [40]. All the results determined from the optical models are summarized in Table 2. It was noted that E_o decreases with increasing the annealing temperature from 100 to 250 ° C which can be related to the observed shift of the optical transmission spectra in the short wavelength region, which in turn shifts the absorption edge toward lower energies.

Fig. 8

	Figure Option ViewDownloadNew Window
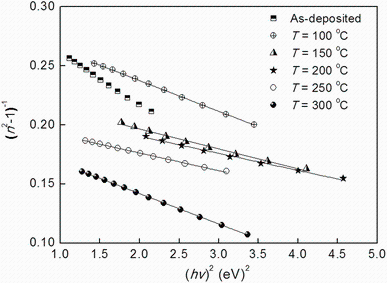	Fig. 8 Plots of (n2 - 1)-1 versus (hν ) 2 for Sn3Sb2S6 thin films as-deposited and annealed at different temperatures

Table 2

Table 2

Table 2 Estimated values of the optical parameters of Sn3Sb2S6 thin films annealed at different temperatures T (° C) Eg(eV) Eo(eV) Ed(eV) ε ∞ M-1 M-3 As-deposited 1.92 3.00 10.00 4.86 0.72 3.33 0.37 100 1.86 3.99 14.28 4.85 0.19 3.57 0.22 150 1.84 3.83 16.66 5.76 1.75 4.34 0.29 200 1.80 2.27 12.50 5.88 1.16 4.54 0.60 250 1.74 2.22 11.11 6.37 1.00 5.00 1.01 300 1.71 3.16 16.66 7.29 2.23 5.27 0.52

Table 2 Estimated values of the optical parameters of Sn3Sb2S6 thin films annealed at different temperatures

The oscillator energy E_o and the interband optical strength E_d are related to the moments of the dispersion spectra M_-1 and M_-3 by the relations [41]:

(12)

(13)

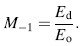
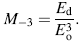
The dependence of the refractive index n on the real dielectric constant is given by the Spitzer-Fan model [42]:

(14)

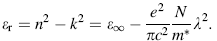
where ε _∞ is the high frequency dielectric constant in the absence of any contribution from free carriers, N/m^* is the ratio of the carrier concentration to the effective mass, c is the speed of light and e is the electronic charge.

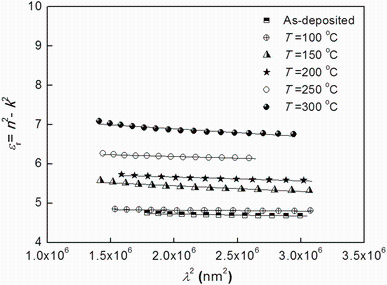
The values of ε _∞ and N/m^* were deduced from the extrapolation of the plots of ε _r versus λ ² to λ ² = 0 and from the slope of the graphs (Fig. 9). These values are listed in Table 2. It can be seen that ε _r increases with the annealing temperature.

Fig. 9

	Figure Option ViewDownloadNew Window
	Fig. 9 Plots of ε r versus λ 2 for Sn3Sb2S6 thin films as-deposited and annealed at different temperatures

3.3.1 Resistivity Measurements

The electrical properties of the thin films are required for the optimization of the preparation conditions to use it in several applications. Electrical characterization of the films annealed at different temperatures was carried out using gold contact. Experimental observations of the thin films resistivity behavior on heating and cooling at different annealing temperatures are detailed. Figure 10a-c shows that the films regained its original resistances, forming a closed hysteresis loop [43], on the completion of the heating-cooling cycle. We found that this result is also for the SnSb₂S₄ and Sn₂Sb₂S₅ thin film materials of the same family [21, 22]. The resistivity decreases with increasing temperature indicating the semiconducting nature of Sn₃Sb₂S₆thin films. The area enclosed by the loop was found to depend on the maximum temperature to which the thin film was heated. In fact, it decreases by rising the annealing temperature which is probably related to the structural changes.

Fig. 10

	Figure Option ViewDownloadNew Window
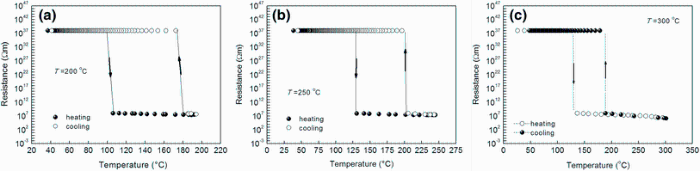	Fig. 10 Variation in the resistivity with the annealing temperatures for the Sn3Sb2S6 thin films annealed at 200 ° C a, 250 ° C b, 300 ° C c

3.3.2 Activation Energy

The analysis of defects in Sn₃Sb₂S₆ thin films was carried out by an examination of activation energy obtained using the relation [44]:

(15)

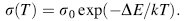
where σ ₀ is a parameter depending on the semiconductor nature, k is the Boltzmann constant and Δ E is the thermal activation energy.

The electrical conductivity as a function of inverse of the temperature of annealed samples is shown in Fig. 11a, b. From the slopes of these graphs, two activation energies are determined. Δ E₁ corresponds to the intrinsic region, and Δ E₂ is probably related to the impurity scattering region [45]. As shown in Table 3, in the higher annealing region (250-300 ° C) Δ E₁ rises while Δ E₂ decreases with increasing temperature by comparison with lower annealing temperature (200 ° C). These results are in good agreement with structural study and indicate that this variation is related to the improvement in crystallization.

Fig. 11

	Figure Option ViewDownloadNew Window
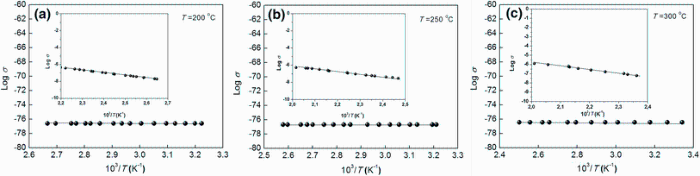	Fig. 11 Plots of ln σ versus 103T103T for the Sn3Sb2S6 thin films annealed at 200 ° C a, 250 ° C b, 300 ° C c

Table 3

Table 3

Table 3 Estimated values of the activation energies of Sn3Sb2S6 thin films annealed at different temperatures T (° C) Δ E1 (eV) Δ E2 (eV) 200 0.28 0.02 250 0.34 0.01 300 0.34 0.01

Table 3 Estimated values of the activation energies of Sn3Sb2S6 thin films annealed at different temperatures