The homogeneous plastic flow in bulk metallic glasses (BMGs) must be elucidated by an appropriate atomistic mechanism. It is proposed that a so-called concordant shifting model, based on rearrangements of five-atom subclusters, can describe the plastic strain behaviour of BMGs in a temperature range from room temperature to the supercooled liquid region. To confirm the effectiveness of the atomic concordant shifting model, a comparative investigation between the vacancy/atom model and the concordant shifting model is carried out based on the estimation of the strain rate deduced from two models. Our findings suggest that the atomic concordant shifting model rather than the vacancy/atom exchange model can well predict the large strain rate in the superplasticity of BMGs.
Bulk metallic glasses (BMGs) can deform plastically by a homogenous flow at a wide temperature range, from Tg (glass transition temperature) to Tx (onset crystallization temperature). Under tensile loading, the result is a continuous elongation with associated transverse contraction, eventually followed by fracture, which has been well documented in the previous studies [1]. The occurrence of the homogeneous flow leads the tensile plastic strain of Pd-based and Zr-based BMGs to be 1260% and 750%, respectively [2, 3]. Based on the compressive tests of BMGs, the stress-strain behaviour of the homogeneous flow is believed to be described by a fictive model [4] or the classic Sellars-Tegart constitutive relationship [5]. As metastable materials, environmental temperature and applied stress during the homogeneous flow can initiate the nanocrystallization of BMGs [6]. Once the nanocrystallization occurs, the homogeneous flow of BMGs will be seriously influenced by the second crystalline phase [7], which can further affect superplastic forming of BMGs [8]. In general, the amount of deformation achieved depends strongly on both the strain rate and the temperature during testing. The characteristic feature of this flow behaviour is exceptional stability that can lead to very large elongations to failure [9]. In crystalline materials, this mode of deformation is known as superplasticity, where it is ascribed to grain boundary sliding that involves atom/vacancy relative motion and dislocation glide [10, 11]. Transmission electron microscopy studies of thin foils prepared from superplastically deformed materials have shown that the grains are relatively dislocation-free because the dislocations climb/glide to the nearest grain boundary when the load is removed and the sample is cooled to room temperature [12]. In this letter, we consider the superplastic deformation of BMGs at temperatures close to Tg. BMGs have no dislocations and no grain boundaries; therefore, the mechanism of homogenous deformation can only occur by one of the two following mechanisms:
1.vacancy-atom exchange, or
2.cooperative atomic motion not depending on vacancies.
As a general rule, close to Tg the fraction of free volume in amorphous solids is in the range from 0.02 to 0.03. Analysis of the above mechanisms in view of the assumed fraction of free volume reveals that the cooperative atomic motion is the only one capable of the high strain rates (~10-3 s-1) observed in experimental measurements. Although recent research has found that the stress wave can make a non-localized viscous flow occurring in BMGs in the supercooled liquid region [13], a quantitative description of the plastic deformation in the atomic scale in a wide temperature range, i.e., from room temperature to glassy transition temperature, is still absent.
The classical model of atom/vacancy pair exchange can be considered as a flow of atoms and vacancies in opposite directions, and it is well documented [14]. Vacancies (on average) have spherically symmetrical tensile stress field around them and, therefore, are attracted towards hydrostatic compression and repelled by hydrostatic tension. For this mechanism to produce elongation in a sample subjected to uniaxial tension, the atoms must flow along the tensile axis towards the top and bottom surfaces of the sample and vacancies towards the side surfaces. The diffusion of one vacancy to the side surface, and one conjugate atom to the top surface, will result in volumetric displacement of the order of d3 (where d is the atomic radius) and contribute to longitudinal strain, with a corresponding strain rate, given by:
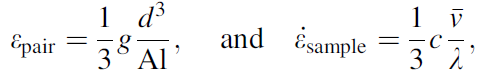 (1)
(1)
where c = nd3/V is the volume fraction of vacancies (free volume), V is the sample volume, n is the number of vacancies, A is the sample cross-sectional area, l is the sample length, λ is the average distance of diffusion, and g ~ 1 is a geometrical packing factor. The average velocity of diffusion of the atom/vacancy pair, v¯ v¯ , can be derived from the diffusion equation: v¯ =3D/λ v¯ =3D/λ , where λ is the average distance of diffusion. The diffusivity constant, D, for atoms in a BMG at 640 K, which is the glassy transition temperature of a Zr-based BMG, is taken to be of the order of 10-19 m2/s [15]. For other quantities, we assume: l = 10 mm, λ = d = 0.2 × 10-9 m, and c = 0.02. Calculations based on these values predict strain rate of 3 × 10-9 s-1.
The original description of vacancy/atom exchange by Spaepen [14] and Eyring [16] includes stress-activated diffusion; therefore, in the above equation, D should be replaced by: D(T) = exp[(Q-σ ω )/RT], with Q being the activation energy for self-diffusion, σ the applied stress, and ω the activation volume. Taking this into account, it is still insufficient to raise the strain rate to an observable regime of 10-5 s-1 [9]. The strain rate calculated from Eq. (1) is at least 4 orders of magnitude lower than those observed in typical experiments. Therefore, other mechanisms of faster flow must be considered to explain the behaviour.
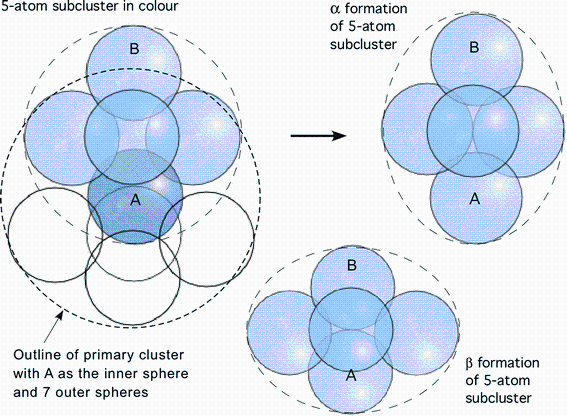
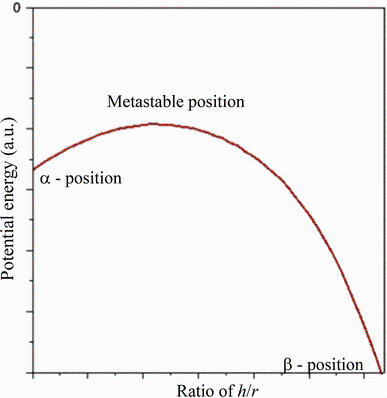
Atomic arrangement in metallic glasses can be represented by an aggregate of irregular primary clusters [17]. An irregular primary cluster can be further subdivided into five-atom subclusters, which are envisaged as the minimum and necessary grouping of atoms capable of permanent plastic deformation (Fig. 1). Within the elastic matrix of the surrounding atoms, the five-atom subcluster can change its shape in response to interaction with an externally applied deformation field. When the “ hard-sphere” packing model is relaxed by the introduction of central atomic force fields, the configuration of the five-atom subclusters tends towards the stable α and β positions and is metastable at some intermediate point as shown in Fig. 2. It is conjectured that the bi-stable action of the five-atom subcluster is the elementary mechanism responsible for atomic rearrangements in amorphous bulk metallic glasses during homogenous superplastic flow. It relies on the elastic compliance of the surrounding matrix to accommodate local displacements and requires no vacancies to operate; every subcluster is a source of concordant deformation. We use the term “ concordant” for this mutually accommodating process of deformation.
The outline of a primary cluster is shown in Fig. 1 by the larger broken line circle. Within that circle, there is a sphere marked A (dark blue), and three of the outer spheres of this cluster are shown in light blue, whilst the remaining spheres of the cluster are drawn schematically by empty circles. There is an atom (sphere) marked B, which belongs to an adjacent primary cluster, but is touching the three outer spheres of the first primary cluster. All five spheres in blue form a five-atom subcluster, outlined by the smaller broken line circle. The whole random packing of atoms in a metallic glass can be thus subdivided into such five-atom subclusters. The five-atom subcluster is envisaged as the minimum and essential group of atoms capable of permanent plastic deformation, activated by stress. In a BMG, the number of different local molecular arrangements is very large and the local configuration will be governed by a probability distribution function [17].
Figure 1 shows an example of the five-atom subcluster transformed into its α formation by elongation along the vertical z-axis, and another one transformed into its β formation by compression along the same axis. It is further envisaged that an amorphous solid has a high density of such effective subclusters and that the process of α ↔ β transformation is regenerative, i.e., it can repeat itself continuously, thus yielding unlimited plastic flow. The process is assisted by density differences between adjacent primary clusters which occur due to variations in coordination number and hence local packing density. However, unlike dislocations that glide on crystal planes with long-range order, the α -β events are not linked in that way, but instead are governed by the local configurations occurring at random throughout the solid.
The displacement field produced by the concordant rearrangement will give rise to some deformation at the surface of the sample. The volume of the inclusion before and after the transformation is the same, i.e., it suffers a change of shape but no change of volume. It is assumed that the transformation of the subcluster from one to the other form can be described by the problem of an inclusion in an elastic matrix, investigated and described by Eshelby [18]. Accordingly, the total elastic strain energy, Uel, of a system comprising an inclusion in an elastic matrix can be expressed by a volume integral:
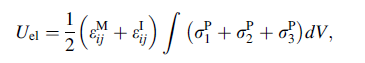 (2)
(2)
where i and j are the coordinates (the position) of the inclusion, 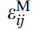
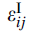
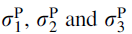
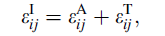 (3)
(3)
where 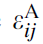
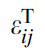
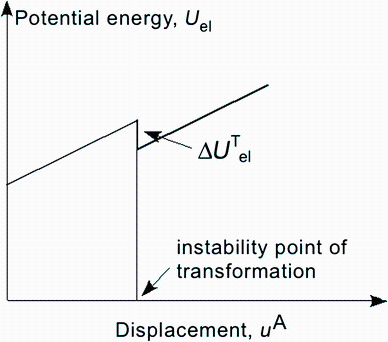 | Fig. 3 Variation of potential energy of the system with applied elongation, manifesting a sudden drop associated with α -β event |
The transformation involves an energy barrier as shown schematically in Fig. 2. It can be observed that in theα formation the subcluster has 9 direct contacts and one separation, whereas in the β formation it has 7 direct contacts and 3 separations. It can be assumed with a degree of certainty that most atomic coordinates change little by this transformation except those in the immediate vicinity of the subcluster. Consequently, the potential energy of the two should differ only by an amount commensurate with the difference in local strain and has an activation energy barrier, as shown in Fig. 2.
Therefore, the properties of the proposed concordant (cooperative) deformation mechanism require:
1.no vacancies (no free volume),
2.every cluster be a potential source of concordant deformation.
The strain rate in Eq. (1) can now be recalculated with new parameters for the concordant mechanism. In particular, the concentration of atoms taking part in simultaneous displacement can be as high as 10%-100%, and the diffusion distance needs to be only of the order of 10-9 nm. Substitution of these new values in Eq. (1) gives predicted strain rate of the order of 10-4 s-1. A comparison of the quantities involved in the two mechanisms is given in Table 1.
| Table 1 Comparison of the two models of homogeneous flow |
It is reasonable to assume that the average velocity, v, of the moving atoms would be the same for both the atom/vacancy and the concordant mechanisms. With this assumption, one can express the ratio of the strain rates for the two cases as follows:
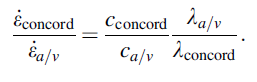 (4)
(4)
The parameters of concentration of defects, c, and the diffusion distance, λ , are listed in Table 1. The vacancies and their conjugate atoms must diffuse through distances commensurate with sample dimensions, whereas in the concordant mechanism the diffusive displacements are only of the order of atomic dimensions. Consequently, the second term on the right-hand side of Eq. (4) is of the order of 105. We estimate the first term to be of the order of 10, giving a factor of 106 for the ratio of strain rates predicted by the two mechanisms. This is the main justification for proposing the concordant shift mechanism of superplastic flow in amorphous metals at temperatures close to the glass transition temperature.
Based on experimental measurements, Yavari et al. [19] showed that free volume in BMGs is dispersed throughout the volume, and atomic-sized vacancies are unstable and non-existent. However, the dispersion of free volume is subject to spatial fluctuations, and the probability of voids in some regions of glass having volume sufficiently close to that of an atom is, therefore, close to one. This supports the possibility of the atom/vacancy diffusion mechanism, although the fraction of vacancies capable of the exchange would be significantly reduced from the 0.02-0.03 value. Another point can be made that vacancies which diffuse to the surface would be depleted during the superplastic flow, apparently without a source generating new vacancies. However, a support for the creation and annihilation of free volume during homogeneous flow in BMGs has been published by Ekambaram et al. [20] and Heggen et al. [21]. This can be understood as atomic rearrangements causing spontaneous local concentration of free volume, thus leading to creation of voids of sufficient size for the atom/vacancy exchange mechanism to operate. They have concluded, though, that the process is inefficient in production of free volume. Another model based on free volume by Ye et al. [22] envisages so-called free volume zones existing in the glassy elastic matrix, presumably created by the above mechanisms. Argon has anticipated the dispersed free volume and proposed a diffused shear zone (STZ) mechanism [23].
The extent of superplastic flow in amorphous metals is strongly dependent on temperature and strain rate [4, 6]. The deformation behaviour changes from plastic to brittle failure as temperature drops below Tg, or as the strain rate increases above a critical value. The ductile-brittle transition is a ubiquitous phenomenon in all materials; the specific molecular mechanism for this transition in BMGs is under continuing investigation [24]. In general terms, one can understand that the rapidly increasing viscosity will require increased levels of stress to affect plastic flow [22], which at some point will become higher than the fracture stress.
Without stress, the glassy solid is believed to have an isotropic structure. However, applying elongation induces anisotropy [25]. The transformation of subclusters into the α form results in altered configurations of the clusters. The calculation of the atomic pair correlation function (PDF) by Fourier transformation of the structure factor becomes direction-dependent and can be expressed by expansion into spherical harmonics. Since the macroscopic behaviour is closely correlated with the medium-range order, we introduce a concept of a concordant region to link the atomic changes at different length scales.
The atomic reorientation in the first nearest-neighbour shell can relax the external stress and reduce the local energy concentration. In order to counterbalance this drop in local stress, other atoms in a surrounding region must bear more stress. In this case, the increment of stress imposed on the surrounding atoms will concordantly shift the atoms in a range corresponding to the length of the stress decay [26]. This shift corresponds to the relaxation process that is necessary to compensate the local stress increment due to the atomic reorientation in the first shell. The concordantly shifting atoms will store the elastic energy until further reorganization occurs. The number of atoms in this volume, i.e., the volume of the associated group of atoms, is an important factor influencing the macroscopic mechanical properties. The development of anisotropy in the structure factor is consistent with the small redistribution of mass under plastic deformation involving theα -β events.
The atoms anisotropically reorientate in the first nearest-neighbour shell, i.e., the α -β event is formed, and the surrounding atoms concordantly and elastically shift, which can be reasonably treated as a core-shell structure. In this structure, the α -β event describes the atomic reorientation, which involves a core, and the surrounding atoms stretch (or shrink) elastically, which is treated as an elastic shell. In the elastic regime, atomic shifting in the core is caged in the elastic shell. A longer-range elastic interaction between neighbouring core-shell structures can deliver the strain and accumulate the elastic energy [27, 28]. Increasing stress causes the quantity of the core-shell structure to increase [25]. When the volume fraction of the core-shell structures reaches a critical value upon increasing the stress to the yield strength, the core (the α -β event) would percolate through the surrounding elastic shells, i.e., cage-breaking takes place, and coalesce to form larger deformation units that are percolation of homogeneously and stochastically deformed clusters [29, 30, 31]. Then, percolated deformation units induce a deformation band formed along the plane with maximum shear stress [32].
The concordant mechanism of plastic flow by the α -β events is capable of predicting large strain rates as observed in experimental testing of BMGs in the superplastic region. By contrast, the vacancy/atom exchange model can only explain creep at relatively low strain rates, but not large strain rate superplasticity in the BMGs.
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|