The vacuum thermal evaporation method was used to deposit Sn₄Sb₆S₁₃ film on corning 7059 glass substrates (10 mm × 20 mm × 1 mm). In our previous researches [6, 7, 13], stoichiometric amounts of the elements of 99.999% purity Sn, Sb, and S via Bridgman method have succeeded the synthesis of Sn _x Sb _y S _z sulfosalt ingots materials. Crushed powders of these ingots were used as a raw material for the thermal evaporation. Thin films of Sn₄Sb₆S₁₃ were sublimated by conventional thermal evaporation technique using high vacuum coating system (Model Alcatel). The evaporator system utilizes two pumps to evacuate the high vacuum chamber, which was made of an enclosed bell jar. Powder of Sn₄Sb₆S₁₃ was used as the evaporation source material. The substrates were placed directly above the source at a distance of 15 cm. The vacuum chamber was evacuated to 1.33× 10^-4 Pa (10^-6 Torr) before the source was heated. The molybdenum boat was heated using 40 A direct current for 10 s to melt the Sn₄Sb₆S₁₃. The current was increased slowly to 90 A until all of the Sn₄Sb₆S₁₃ evaporated. The films were removed after waiting for a few hours for the chamber to cool down. The films were deposited onto clean corning 7059 glass substrates for optical measurements; the corning 7059 glass substrates were carefully cleaned by chromic acid for 15 min and then rinsed by deionized water. The material was sublimated from a heated molybdenum boat in a vacuum of 1.33 × 10^-3 Pa (10^-5 Torr). The substrate temperature controlled by a chromel-alumel thermocouple was varied from 30 to 200 ± 5° C. Substrate heating was performed by an electrical heater. The optimized deposition parameters such as molybdenum boat-substrate distance (10 cm) and evaporation time (20 min) were kept constant. In the end of the evaporation process, the heater was slowly closed, and the glass substrates were given up cooling for 1 h in vacuum. For each substrate temperature, the structure, morphological, and optical properties of the produced films were investigated.

The crystal structures of the samples were analyzed using a Philips X’ Pert X-ray diffractometer in Bragg-Brentano geometry (θ /2θ ) with CuKα radiation (λ = 0.154056 nm and 40 kV, 30 mA) in the range 2θ = 20° -70° . The surface morphology of the films was investigated using the atomic force microscopy (AFM, Vecco model D 3100). The transmittance T(λ ), the reflectance R(λ ), and the spectra of Sn₄Sb₆S₁₃ thin films were measured at normal incidence of light in the spectral range 300-1800 nm using a double-beam spectrophotometer (SHIMDZU model UV 3100S). An uncertainty of 1% was given by the manufacturer for measurements obtained by this spectrophotometer. A glass substrate, such as that used for thin film deposition, was used as a reference for transmittance and reflectance scan. Film thickness was calculated from the positions of interference maxima and minima of reflectance spectra using a standard method [14]. The film thickness was controlled and monitored during the evaporation process by using a quartz crystal sensor (Model, TM-350 MAXTEK, Inc., USA). The deposited films have a thickness in the wavelength range 400-540 nm.

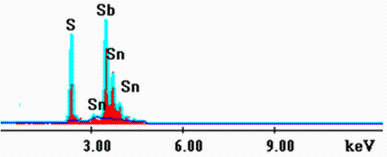
Energy-dispersive X-ray (EDX) analysis was used to determine the elements composition in typical Sn₄Sb₆S₁₃ thin film. The result is shown in Fig.1. The spectrum of the film deposited at T_s = 30° C shows only S, Sn, and Sb elements, indicating the purity of the synthesized film. This result provides the elemental composition and the average atomic percentage of the Sn₄Sb₆S₁₃ film deposited at T_s = 30° C, showing a high average atomic percentage of S (54.4%) compared to both Sn and Sb (12.8% and 32.8%).

Fig.1

	Figure Option ViewDownloadNew Window
	Fig.1 EDX measurements of the Sn4Sb6S13 thin films deposited at 30° C

3.2.1 Powder X-ray Diffraction

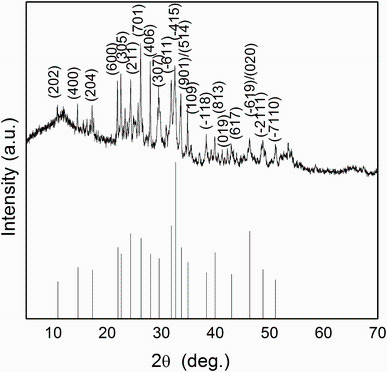
The powder profile of Sn₄Sb₆S₁₃ material is shown in Fig.2. The pattern exhibits well sharp and intense peaks, which is a signature of crystalline phase of prepared Sn₄Sb₆S₁₃. The powder X-ray diffraction data are indexed to be a monoclinic crystal system. The lattice parameters a, b, c, and β are calculated by using the following relation:

dhkl=1(b2a2+l2c2-shlaccos⁡(β))1sin⁡2(β)+k2b2 (1)

Fig.2

	Figure Option ViewDownloadNew Window
	Fig.2 X-ray diffraction patterns of standard and as-synthesized Sn4Sb6S13 powder

The corresponding lattice cell parameters are evaluated: a = 2.438 nm, b = 0.392 nm, c = 2.288 nm, and β = 91.19° . These results are in good agreement with those in JCPDS Card No. 74-0676 (a = 2.431 nm, b = 0.391 nm, c = 2.349 nm, and β = 94.05° ). The peak positions shown in Fig.2 match well with those in the standard pattern (JCPDS Card No. 74-0676).

3.2.2 X-ray Diffraction of Sn₄Sb₆S₁₃ Films

Figure 3 shows the XRD patterns of a Sn₄Sb₆S₁₃ thin film at various substrate temperatures. The reflections illustrate a strong peak of Sn₄Sb₆S₁₃, corresponding to the (6¯11)plane. The weak ( 4¯02) diffraction peak of Sn₄Sb₆S₁₃ appeared at a substrate temperature of 100° C, and no other peak was detected. Usually, semiconductor materials deposited by thermal evaporation method at room temperature present dominant amorphous component. Figure 3 presents an extraordinary result of the deposited Sn₄Sb₆S₁₃ film crystallized in spite of low substrate temperature (room temperature 30° C). Similar results were also observed by other researchers [6, 7]. All films are preferentially oriented along ( 6-11) plane. It is obvious that the intensity of the peak corresponding to ( 6-11) plane increases with the rise in the substrate temperature. This behavior shows that with heated substrates the crystalline quality of Sn₄Sb₆S₁₃ layers is enhanced. To get more structural information by exploiting X-ray diffraction patterns of Sn₄Sb₆S₁₃ compound, the microstructural parameters, i.e., crystallite size, lattice strain, and dislocation density, have been estimated. The average crystallite size of synthesized samples was calculated by applying the Scherrer’ s formula:

Fig.3

	Figure Option ViewDownloadNew Window
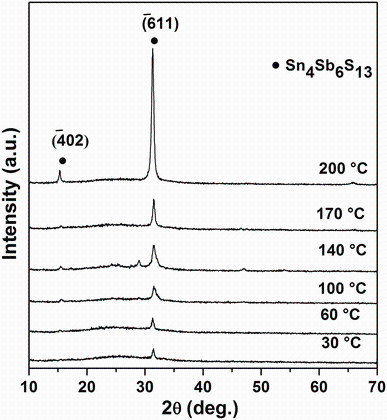	Fig.3 X-ray diffraction patterns of Sn4Sb6S13 thin films deposited on glass substrates heated at different temperatures

D=kλβcosθ(2)

where k is a constant (a shape factor whose value is about 0.9), λ is the wavelength of X-ray radiation (0.15405 nm) used, β is the full width at half maximum (FWHM) intensity of the diffraction line, and θ is the diffraction angle. By increasing substrate temperature from 30 to 200° C, we note that the crystallite sizes of the samples increase from 20 to 48 nm and the FWHM of the ( 6-11). diffraction peak of samples decreases from 0.41° to 0.17° . This implies that the crystallization degree is improved and indicates that the prepared Sn₄Sb₆S₁₃ material contains nano-crystallites. The increase in the grain size is related to the arrangement and coalescence of small grains at low substrate temperature, and because of their limited mobility, the adatoms remain in the substrate where they form smaller nuclei. With increasing substrate temperature, atoms become more mobile, which leads to obtain larger grain size [15]. The lattice strain ε is defined as the disarrangement of lattice created during deposition process and was determined by using the Scherrer’ s relation [16]:

D=β4tanθ(3)

The lattice strain values were in the range of 6.38 × 10^-4-2.65 × 10^-4. We remark that the micro-strain decreases with increasing substrate temperature. This change may be explained by the decrease in concentration of lattice imperfections related to the growth in the grain size.

The dislocation density (δ ) is defined as the length of dislocation line per unit volume of crystal. It was calculated from the formula [17]:

δ=1D2(4)

The calculated dislocation density varied in the range of 25 × 10¹⁴-4.33 × 10¹⁴ (lin. m^-2) and is decreasing with increasing substrate temperature. This result indicates that the layers become more relaxed due to reduction in defects in the structure. This suggests the improvement in film crystallinity by increasing substrate temperature. The number of crystallites per unit area can then be evaluated using the following relation [18]:

δ=1D3(5)

where t is the film thickness. The estimated number of crystallites per unit area is varied between 67.2 × 10¹⁵ and 3.6 × 10¹⁵ per unit area with substrate temperature. This increase can be attributed to grain agglomeration. First, at low substrate temperature, the Sn₄Sb₆S₁₃ thin films are composed of large number of small grains. Then, by increasing substrate temperature the small grains become greater. The calculated values of microstructural parameters are summarized in Table 1. It is clearly observed that substrate heat treatments improve the crystallinity of films.

Table 1

Table 1

Table 1 Structural parameters and surface roughness of Sn4Sb6S13 films deposited at different substrate temperatures Ts (° C) FWHM (° ) Crystallite size, L (nm) Strain ε × 10-4 Number of crystallites per unit area (1015 N) Dislocation density δ × 1014 (lin. m-2) Roughness (nm) AFM Optical 30 0.41 20 6.38 67.2 25.00 2.81 4.08 60 0.36 22 5.62 37.9 19.15 3.76 4.36 100 0.35 23 5.50 35.9 18.53 4. 53 4.77 140 0.29 28 4.55 16.8 12.54 5.84 6.30 170 0.29 29 4.40 18.4 12.05 6. 95 7.21 200 0.17 48 2.65 3.6 4.33 8.23 8.43

Table 1 Structural parameters and surface roughness of Sn4Sb6S13 films deposited at different substrate temperatures

3.2.3 AFM Analysis

Figure 4 shows two-dimensional (2D) and three-dimensional (3D) surface morphology images of Sn₄Sb₆S₁₃ thin films deposited at different substrate temperatures. The scanning area was 1.0 μ m × 1.0 μ m in tapping mode. The root-mean-square roughness (RMS) and the grain size were determined by using standard software (WS × M 5.0 software) [19]. It is clearly observed that the films deposited at various temperatures showed different surface roughnesses. The films deposited at room temperature and at 60° C show a dense and smooth surface due to poor crystallinity. However, at substrate temperature higher than 100° C the surface becomes homogeneous and constituted of densely packed grains. The crystallites have spherical form and uniform distribution. The AFM measurements indicate that the RMS of all samples increases from 2.81 to 8.23 nm. This is caused by the rise in substrate temperature from 30 to 200° C (Table 1). The surface roughness of the films was also evaluated by using an optical method based on the spectrophotometric data following this formula (σ ≪ λ ) [20]:

RSRT=exp⁡exp-(4πσλ)2+1-(4πσλ)2×[1-exp⁡[-(βπσuλ)2]] (6)

Fig.4

	Figure Option ViewDownloadNew Window
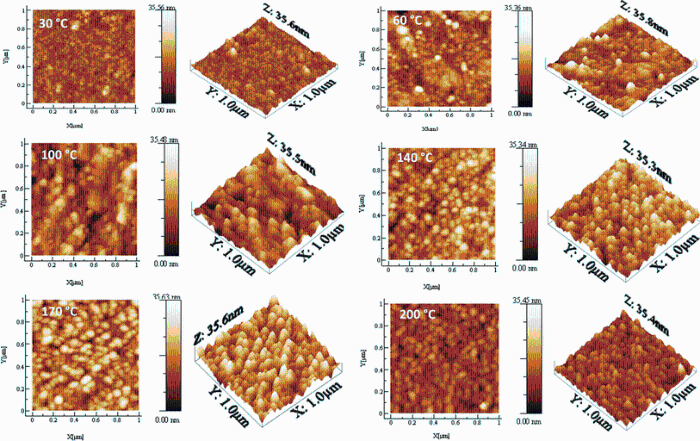	Fig.4 2D and 3D AFM micrographs (1μ m × 1 μ m) of Sn4Sb6S13 thin films deposited on glass substrates heated at different temperatures

where R_S is the specular reflection, R_T is the total reflection of the films, and σ , μ are the average roughness of the irregularities, respectively, the highest and the lowest. The total reflection R_T equals the sum of R_S and R_diff (diffuse reflection). The diffuse and the specular reflection data of Sn₄Sb₆S₁₃ films were measured by a UV-visible-NIR spectrophotometer in the spectral range of 300-1800 nm. Equation (6) is formed by two terms. The first defines the coherent part of reflection, while the second term represents the incoherent part. If the second term is negligible, a new expression of the relation (7) is obtained [21]:

ln/RS\RT=-4πσλ2+A(7)

where A is a constant from the spatial fluctuations of the optical constants. Thus, by plotting ln(R_S/R_T) versus 1r2, the RMS values of the surface roughness of layers were calculated. The obtained values are given in Table 1. It is observed that the estimated value of the surface roughness from both methods increases with increasing heating substrate. Thus, with increasing substrate temperature, the defects decrease and grain sizes become larger so crystallinity is improved. This result agrees with the XRD observation.

3.3.1 Optical Transmittance and Reflectance Spectra

Figure 5a, b shows the typical transmittance T(λ ) and reflectance R(λ ) spectra of Sn₄Sb₆S₁₃ thin films grown at different substrate temperatures in the wavelength range of 300-1800 nm. It is clear that all films exhibit two distinct slopes. The first one (900-1800 nm) is commonly named the transparency zone in which multitude interference fringes are seen showing fairly homogenous films. In this region, all films exhibit a good transparency (70%-80%) in the visible and infrared regions. However, a small decrease in the transmission by increasing the substrate temperature was observed in the spectral range 900-1800 nm. The second region (300-900 nm) is well known by the zone of high absorption. In this spectral region, the signal is strongly reduced at the band edge, especially at 200° C. In this spectral range, an increase in the rate values of reflection of 30% for substrate temperature of 200° C was also observed, which can be explained by a decrease in the absorption phenomena reducing the performance of this material in this region.

Fig.5

	Figure Option ViewDownloadNew Window
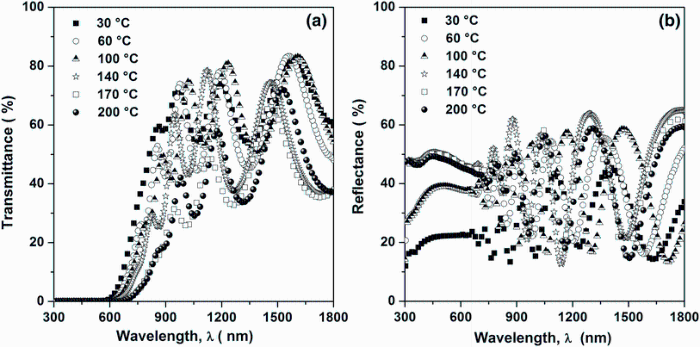	Fig.5 Optical transmission a and reflection b spectra of Sn4Sb6S13 thin films deposited on glass substrates heated at different temperatures

3.3.2 Absorption Coefficients, Energy Gap, and Refractive Index

The optical absorption coefficient was evaluated from the transmittance T(λ ) and reflectance R(λ ) data by using the following formula [22, 23]:

α=1dln/(1-R)2\T (8)

where d is the film thickness. Figure 6 shows the dependence of the absorption coefficient on photon energy for Sn₄Sb₆S₁₃ films deposited at different substrate temperatures. It can be seen that all the Sn₄Sb₆S₁₃ films have relatively high absorption coefficients which are higher than 10⁵ cm^-1 in the visible and the near-IR spectral regions. This result is very important because the spectral dependence of the absorption coefficient affects the solar cell conversion efficiency in photovoltaic applications. The dependence of the absorption coefficient on photon energy is analyzed in the high absorption regions to achieve detailed information about the energy band gaps. The absorption coefficient and photon energy can be related by applying the model postulated by Tauc [24], Davis and Mott [25] independently:

Fig.6

	Figure Option ViewDownloadNew Window
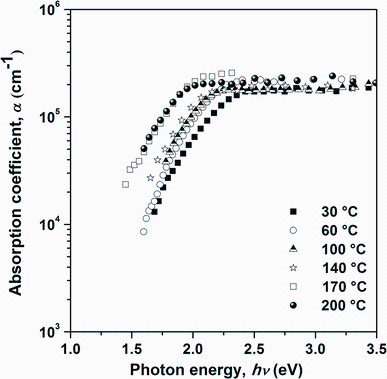	Fig.6 Absorption coefficient α of Sn4Sb6S13 thin films deposited on glass substrates heated at different temperatures

(αhν)n=A(hν-Eg). (9)

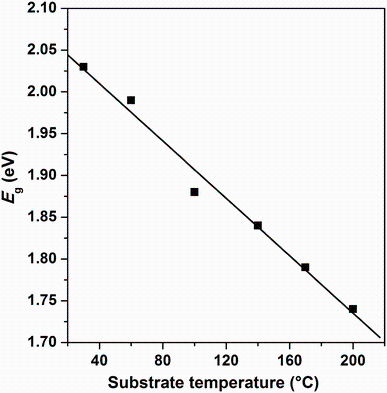
where A is a constant, E_g is the optical band gap, h is the Planck constant, and n is an index that characterizes the optical absorption process. In theory, n equals 1/2, 2, 3, and 3/2 for indirect allowed, direct allowed, indirect forbidden, and direct forbidden transition, respectively. In Fig.7, (α hν )² versus hν is plotted in order to extract direct band gap values by extrapolating the linear regions of (α hν )² to the horizontal photon energy axis. The direct band gap energy tends to decrease from 2.03 to 1.69 eV with increasing substrate temperature. Figure 8 shows the variation of optical band gap E_g versus substrate temperature. The decrease in E_g to 1.69 eV by increasing substrate temperature may be explained by the enhancement of crystallite size and the decrease in defects [2]. This result was proved by many other studies of Sn₃Sb₂S₆, SnSb₄S₇, and Sn₂Sb₆S₁₁ deposited by the same technique and in the same condition [26, 27]. Due to the existence of the interference patterns, this exhibits several maxima and minima as the wavelength increases, and the method of Swanepoel [28, 29] was used to calculate the refractive index n. The method is based on the approach of Manifacier et al. [30]. This approach offers a creation of upper and lower envelope for transmission spectrum beyond the absorption edge. The refractive index can then be calculated from the relation [28, 29]:

n={N+(N2-ns2)1/2}1/2 (10)

Fig.7

	Figure Option ViewDownloadNew Window
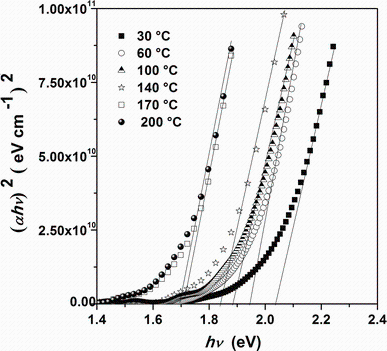	Fig.7 Plot of (α hν )2 versus photon energy (hν ) for Sn4Sb6S13 thin films deposited on glass substrates heated at different temperatures

Fig.8

	Figure Option ViewDownloadNew Window
	Fig.8 Variation of band gap energy Eg versus substrate temperature for Sn4Sb6S13 thin films

N=2nsTM-TmTMTm+ns2+12(11)

where n_s is the refractive index of glass substrate. T_M and T_m are the values of the envelope at the wavelengths where the upper and lower envelops and the experimental transmittance spectrum are tangential, respectively. The variations of refractive index n versus wavelength of the Sn₄Sb₆S₁₃ films deposited at different substrate temperatures are shown in Fig.9. As observed, the refractive index is influenced by substrate temperature and shows normal dispersion behavior. Indeed, n decreases with increasing wavelength of incident photon and tends to be constant at higher wavelengths. The dispersion spectra of refractive index were fitted using the Cauchy formula [31]:

Fig.9

	Figure Option ViewDownloadNew Window
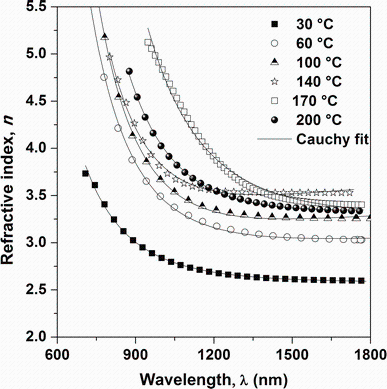	Fig.9 Variation of refractive index n vs wavelength and the fit with Cauchy’ s formula for Sn4Sb6S13 thin films deposited at different substrate temperatures

nλ=n0+Aλ2+Bλ4 (12)

where A and B are the Cauchy’ s parameters and λ is the wavelength of light used. For λ → ∞ , the significance of the n₀ appears immediately as n_∞ . Figure 9 shows the variation of n with Cauchy fitting for as-deposited Sn₄Sb₆S₁₃ thin films at different substrate temperatures. It is clear that the values of n for all the investigated samples obey the Cauchy law. The values of fit parameters and n₀ are presented in Table 2. There is a good correlation between refractive index and optical band gap of semiconductors, where typically, n increases as E_g decreases. The same result is obtained by others study of SnSbS thin films grown by vacuum evaporation method [7]. Since E_g decreases with substrate temperature, the temperature dependence of n arises from the variation of E_g with the substrate temperature which can be correlated to the improvement in film crystallinity. Therefore, energy band gap decreases and refractive index increases with decreasing substrate temperature, which can be related to the film crystallization [32]. The refractive index dispersion has an important role in the research for optical materials due to a significant factor in optical communication and in designing devices for spectral dispersion. The dispersion was analyzed using the model of single oscillator and can be expressed by the Wemple-DiDomenico relationship as follows [33, 34]:

Table 2

Table 2

Table 2 Results concerning Cauchy parameters and refractive index n(0) at zero photon energy Ts (° C) A (nm-2) B (1012 nm-4) n0 (Cauchy) n(H-V) 30 -119, 842 0.36 2.59 2.58 60 -772, 309 1.05 3.18 3.04 100 -1, 268, 800 1.38 3.54 3.24 140 -1, 501, 720 1.41 3.90 3.53 170 -792, 455 2.23 3.38 3.39 200 -958, 282 1.48 3.50 3.33

Table 2 Results concerning Cauchy parameters and refractive index n(0) at zero photon energy

n2hν=1+E0EdE02-(hν)2(13)

where hν is the photon energy, n is the refractive index, E₀ is oscillator energy, and E_d is the dispersion energy. E_d allows evaluating the average force inter-band optical transition. Wemple and DiDomenico have related this parameter to the coordination number for anion and the valence electron number per anion. E₀ and E_d values are obtained from the intercept E₀/E_d and the slope (E₀E_d)^-1by extrapolating the curve representing the plot of (n²-1)^-1 versus (hν )² (Fig.10). The refractive index n(0) at zero photon energy, which is defined by the infinite wavelength dielectric constant, can be deduced from the dispersion relationship by extrapolation of the linear part (n²-1)^-1 versus (hν )². The values of n₀ found by the Cauchy fitting and the Wemple-DiDomenico model are in good agreement. Dielectric constants are linked to the refractive index n and allow us to further analyze the optical properties of samples. The dependence of refractive index n on the real dielectric constant is expressed by the Spitzer-Fan model [35]:

Fig.10

	Figure Option ViewDownloadNew Window
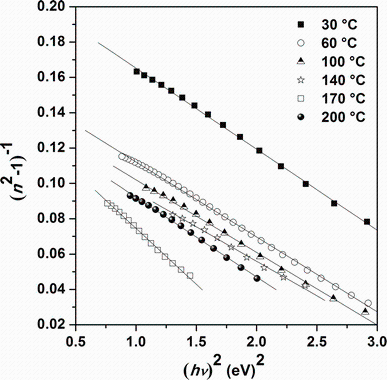	Fig.10 Plot of (n2-1)-1 versus (hν )2 for Sn4Sb6S13 thin films deposited at different substrate temperatures

ε _r=n²-k²=ε _∞ - e2πc2Nm* λ2(14)

where ɛ _∞ is the high-frequency dielectric constant in the absence of any contribution from free carriers, N/m^* is the ratio of the carrier concentration to the effective mass, c is the speed of light, and e is the electronic charge. ɛ _∞ and N/m^* were deduced from plotting ε _r. versus λ ² (Fig.11) and fitting to a straight line. It is important to compare the values of ɛ _∞ achieved from the Wemple-DiDomenico model (Fig.10) with that obtained from the Spitzer-Fan model (Fig.11). Indeed, the two models show satisfactory agreement. On the other hand, the electrical susceptibility χ _e owing to the inter-band transitions of free carriers can be obtained from the optical constants and is determined as:

e2πc2Nm* λ2=-4πχe (15)

Fig.11

	Figure Option ViewDownloadNew Window
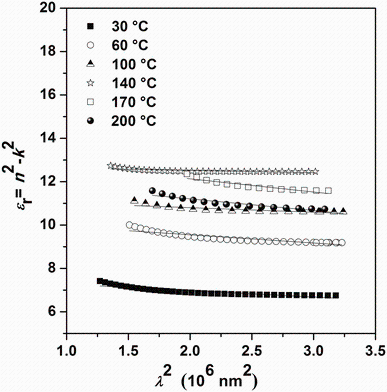	Fig.11 Plot of ε r versus λ 2 for Sn4Sb6S13 thin films deposited at different substrate temperatures

Plots of -4πχe versus photon energy λ2for the deposited Sn₄Sb₆S₁₃ thin films are shown in Fig.12. The figure depicts that χe increases in magnitude with the wavelength and becomes sufficiently large to reduce the refractive index and dielectric constant in the near-infrared region. A good fit to a straight line is seen from which the free carrier susceptibility values at the extremes of the investigated range were estimated. All the results determined from the two models for both samples are summarized in Table 3.

Fig.12

	Figure Option ViewDownloadNew Window
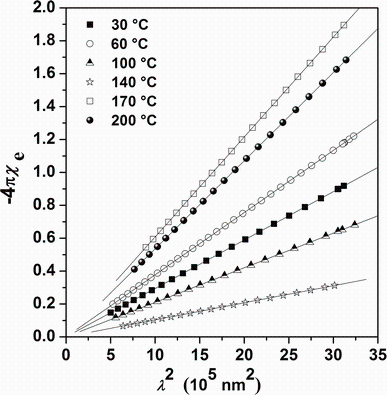	Fig.12 Plot of -4πχe versus λ 2 for Sn4Sb6S13 thin films deposited at different substrate temperatures

Table 3

Table 3

Table 3 Values of the dispersion energy (Ed), oscillator energy (E0), ratio of the carrier concentration to the electron effective mass (n/m* ), the lattice dielectric constant (ε ∞ ), and electrical susceptibility χe as a function of substrate temperature of Sn4Sb6S13 thin films T (° C) E0 (eV) Ed (eV) E0/Eg (eV) N/m* (1048 cm-3) ε∞S ε∞w - χe (10-2) 30 2.15 10.16 1.06 3.24 7.56 5.72 1.19-07.40 60 1.91 12.35 0.96 4.17 10.30 7.46 1.51-09.71 100 1.86 13.03 0.99 2.31 11.22 8.00 0.87-05.41 140 1.85 13.8 1.01 1.14 12.72 8.45 0.55-02.46 170 1.48 10.69 0.83 6.70 13.34 8.22 4.29-14.96 200 1.74 12.70 1.00 5.91 12.27 8.29 3.18-13.37

Table 3 Values of the dispersion energy (Ed), oscillator energy (E0), ratio of the carrier concentration to the electron effective mass (n/m* ), the lattice dielectric constant (ε ∞ ), and electrical susceptibility χe as a function of substrate temperature of Sn4Sb6S13 thin films